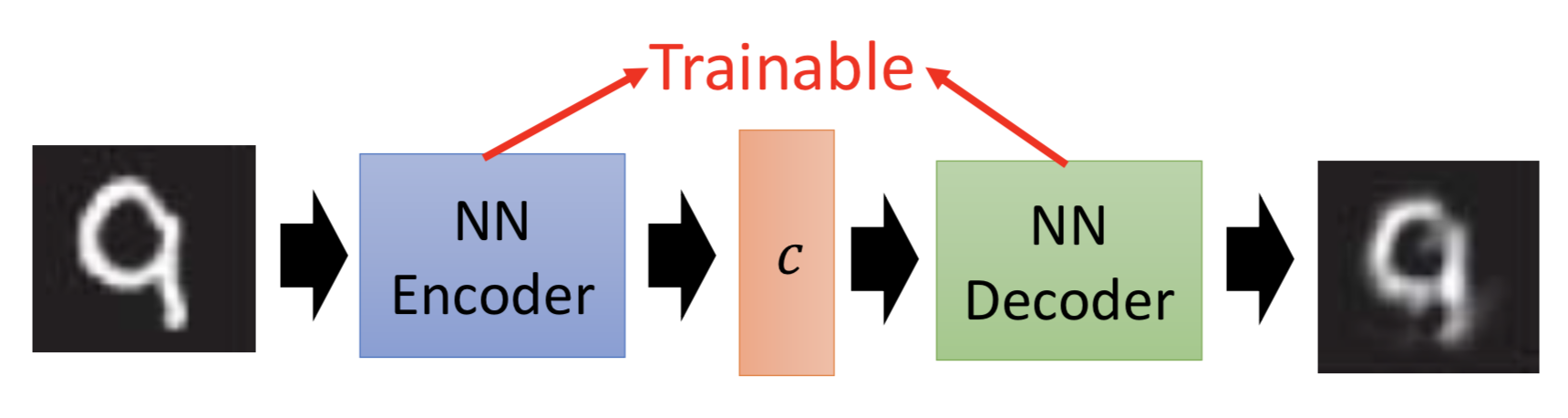
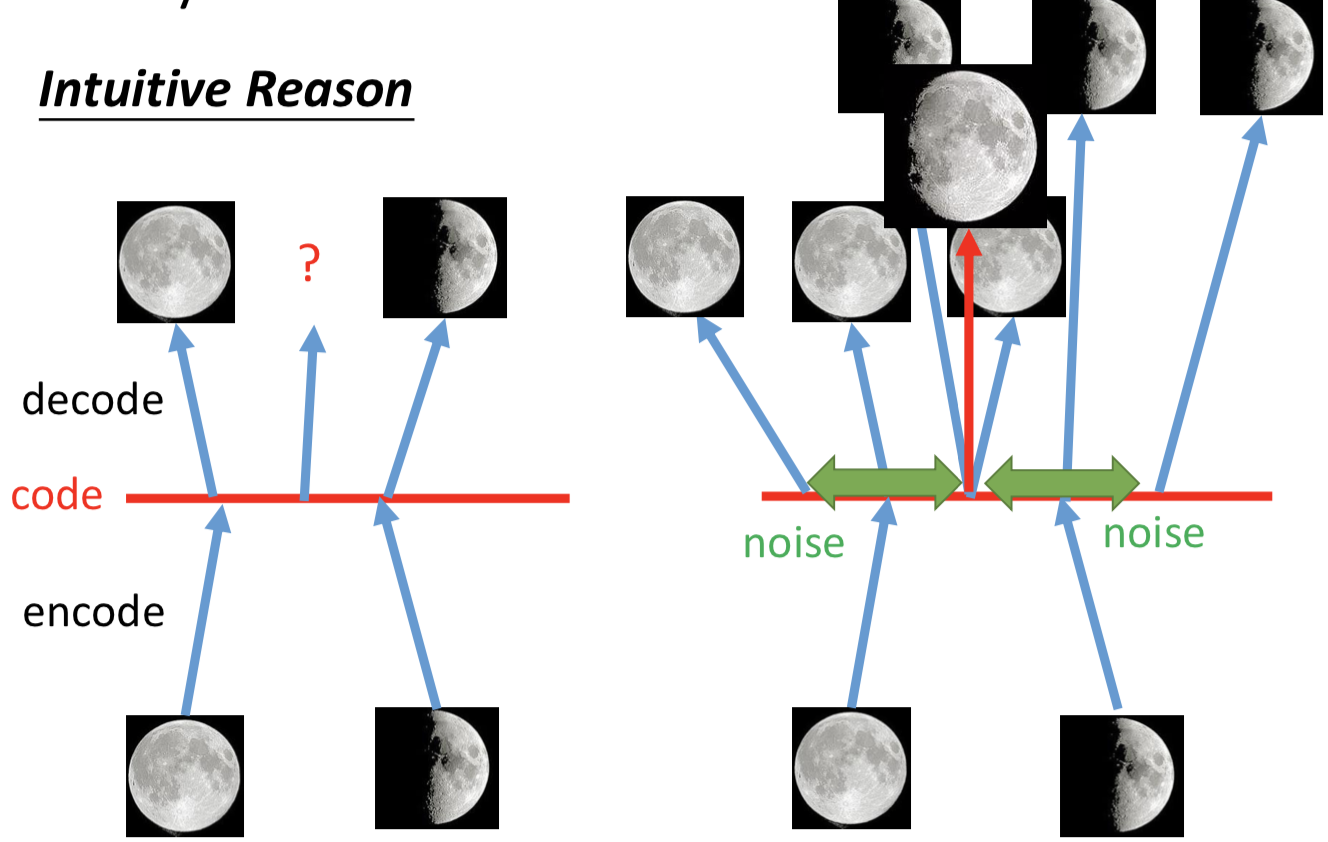
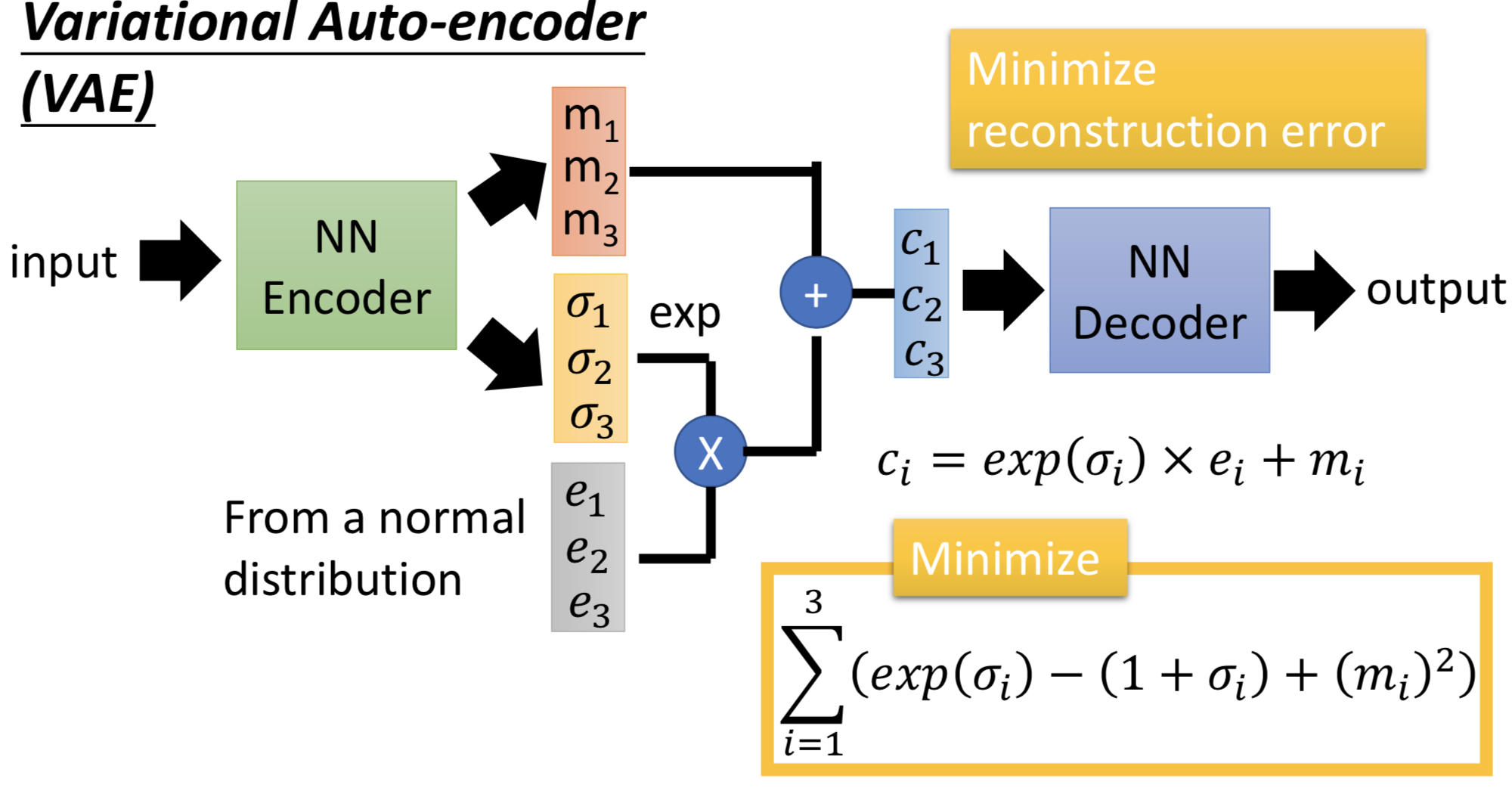
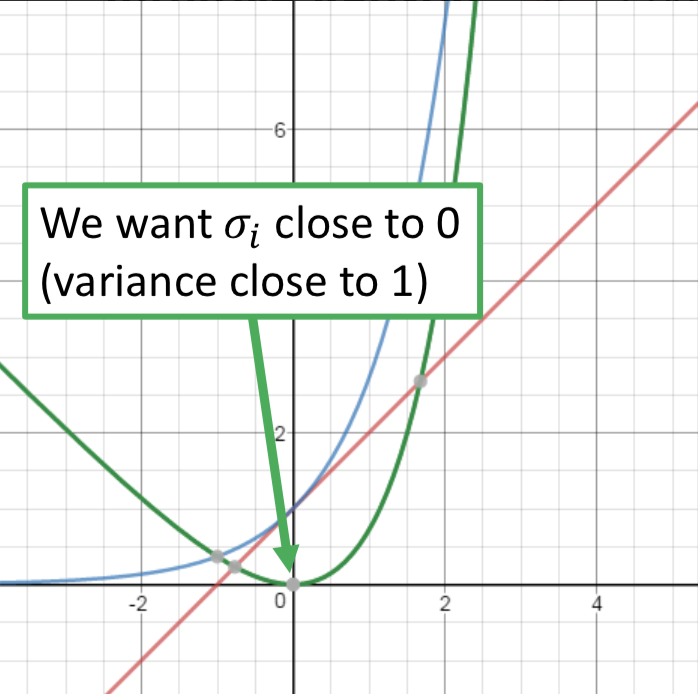
因此在VAE中,encoder输出的不直接是code,而是一组m和一组σ,而向量c才是真正的加了噪声的code,其中ci = exp(σi) x ei + mi。训练过程中的优化目标也不仅是重构误差,还有一项 Σ (exp(σi) - (1+σi) + (mi)2),要强迫加的噪声的方差不能太小(因为是模型学习的参数,如果不做限制,为了能重构的更好,会越更新σi 越使得噪声方差接近0;而实际上我们希望σi 接近0(真正的方差接近1),所以最小化exp(σi) - (1+σi),mi平方项可以理解为L2 norm正则)。
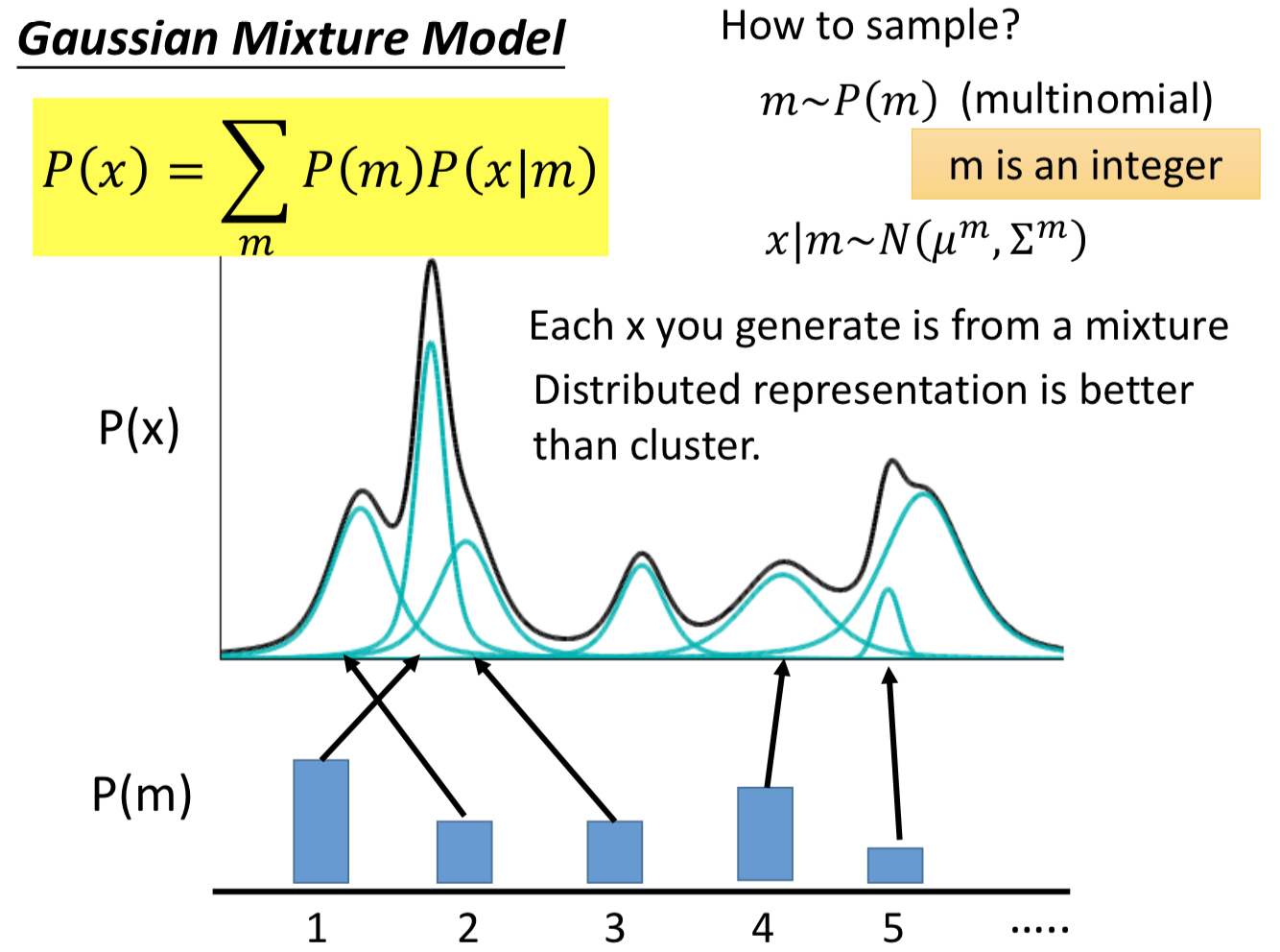
而 VAE 实际上就是GMM的 distributed representation 的版本,先从一个高斯分布中采样出一个向量 z, z 的每个维度就表示某一种特性,再根据 z 来决定高斯分布的 μ 和 σ。由于 z 是连续的,所以有无穷多个z,就有无穷多个高斯分布(在GMM中有几个高斯就是固定的)。在z的空间中,每个点都可能被sample到,而每一个点都对应到一个不同的高斯分布。
那么如何得到 z 和高斯的 μ 和 σ之间的对应关系呢?干脆就用一个NN来描述 μ(z) 和 σ(z) 的函数关系。

所以在整个 VAE 模型中,关键不是使用 p(z)(先验分布)是正态分布的假设(z服从别的分布也可以),而是假设 p(z | x)(后验分布)是正态分布(GMM)。
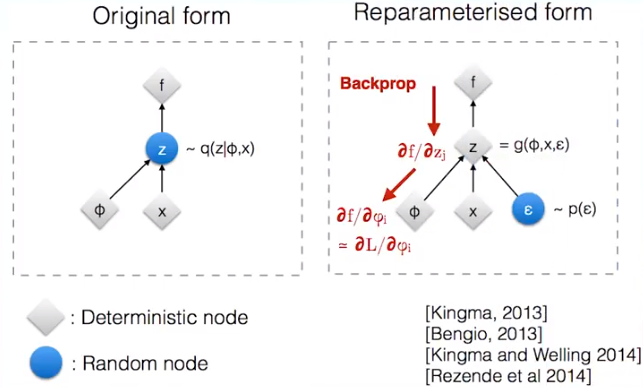
但直接这样处理的话会导致梯度更新出现问题。因为 z 要从后验分布中 sampling 得到,这种随机性会导致 encoder-decoder 不可微。所以采用 re-parameterization trick ,引入一个新的变量来表示不确定性,把采样过程移出计算图,就可以梯度更新了,而新引入的变量处理为一个 weight 固定的输入。例如下图,本来是想要从 N(x, Φ2) 中采样 z ;现在从 N(0, 1) 中采样得到 ε , 然后令 z = x + ε*Φ 即可。
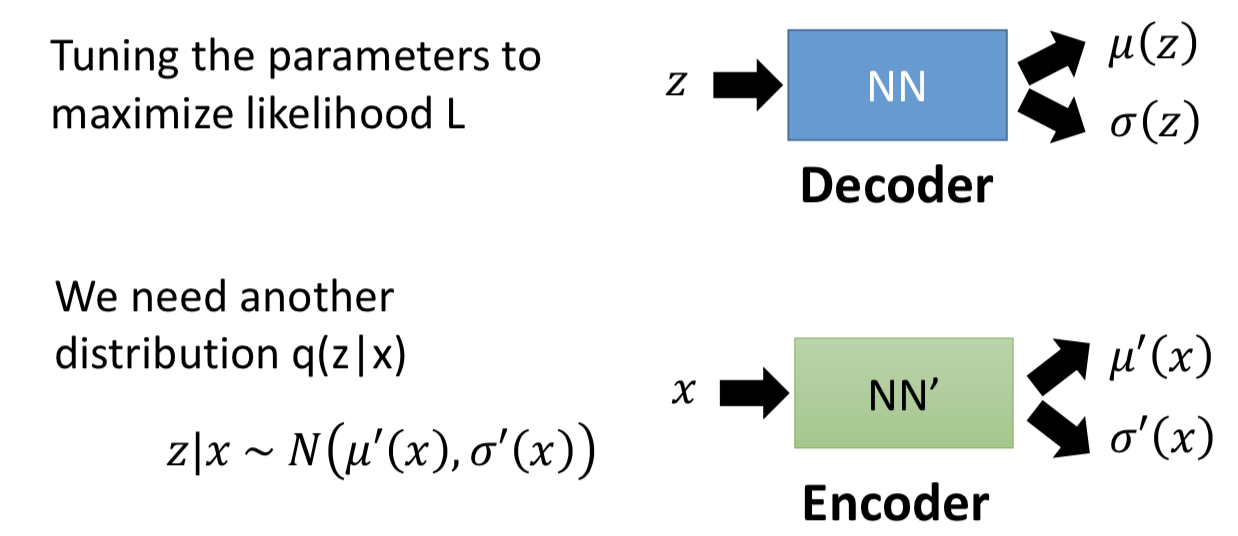
回到 VAE 的目标函数。估计 μ(z) 和 σ(z) 的方法就是最大似然估计,令 μ(z) 和 σ(z) 的取值使得对手上所有的数据x的似然越大越好。

任务就是要通过极大似然估计来更新 μ(z) 和 σ(z) 这两个函数,也就是更新对应的NN参数(decoder)。此外引入一个任意的分布 q(z | x),作用接下来再说,它也是由一个NN来表示。
接下来求解 log p(x),先引入一个任意的分布q(z | x)再把它积掉,其中 p(x) = p(x, z)/p(z | x),代入展开,发现对数似然函数的下界。

如果只是优化 p(x | z) 令 Lb 变大,虽然下界变大了,但 log p(x) 整体却不一定变大,因为不知道log p(x) 和 Lb 之间的差距是多少。引入 q(z | x) 的目的就在于,如果固定 p(x | z) 优化 q(z | x) 令下界变大,由于 q(z | x) 和 p(x) 无关,所以 log p(x) 的值不会改变,那么当Lb 变大,q(z | x) 和 p(z | x) 的 KL散度就会变小,理想情况下 q(z | x) 和 p(z | x) 一致,Lb 变大到和 log p(x) 相等,这时候如果再优化 p(x | z) 令Lb 变大,那么 log p(x) 就一定会随之变大。

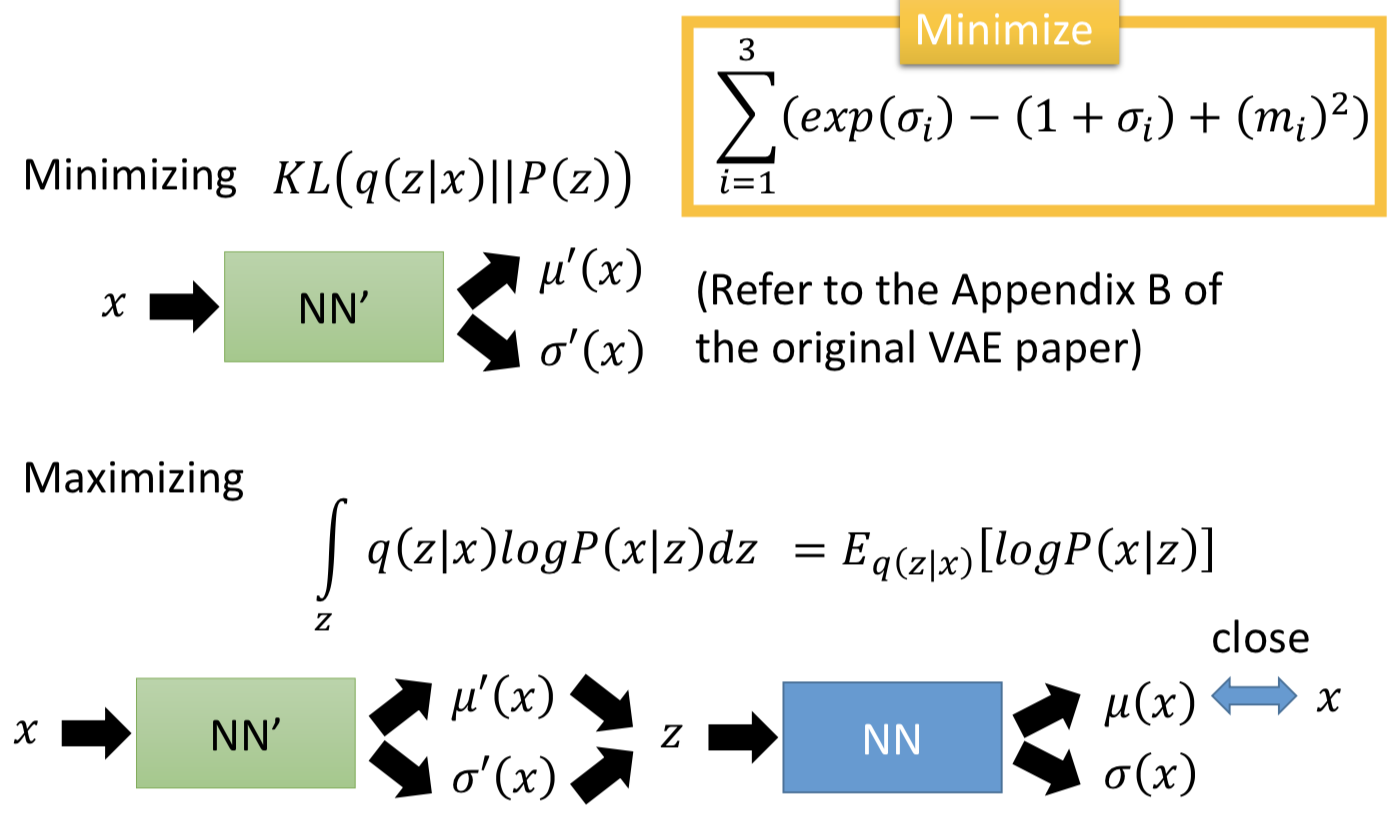
然后展开 Lb 看如何最大化它,其中第一项为 - KL(q(z | x) || p(z)),最大化 Lb 的过程中,q(z | x) 和 p(z) 的 KL散度会最小化(q(z | x) 会越来越接近 p(z)),这就是 VAE 目标函数中 Σ (exp(σi) - (1+σi) + (mi)2) 的作用。
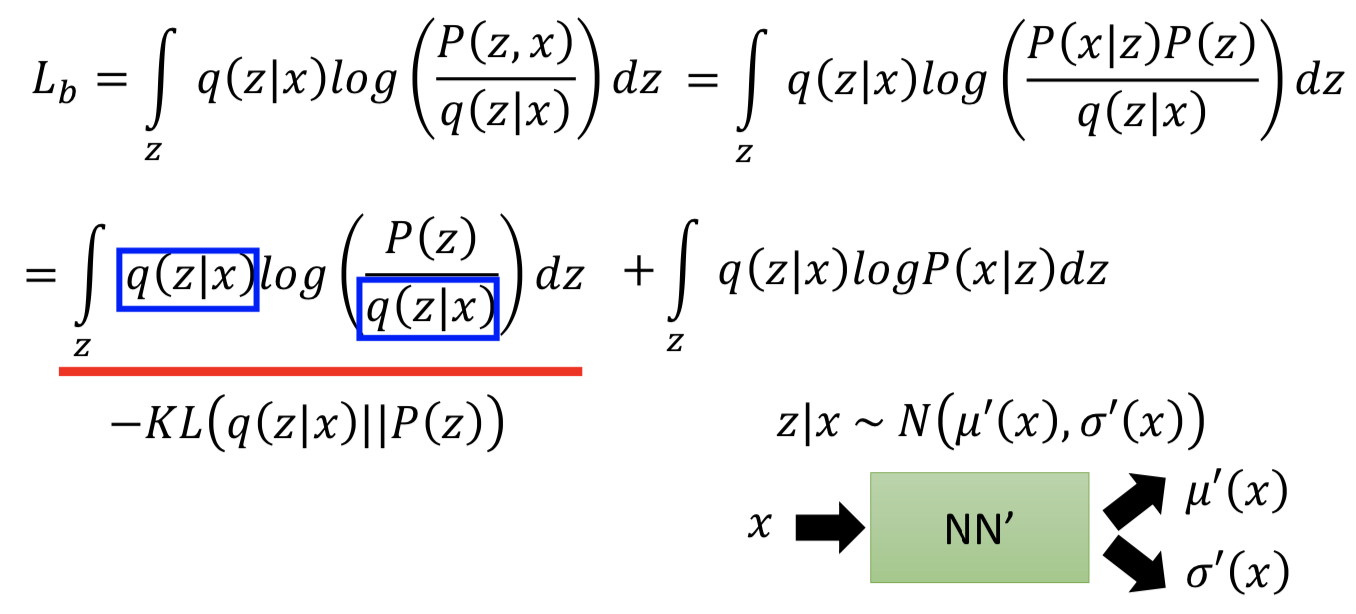
而最大化第二项即为最大化 Eq(z | x)[logp(x | z )],也就是给定一个 x , 根据 q(z | x) 来 sample 一个 z,然后要最大化log p(x | z) 。这就是 autoencoder 的拓扑结构的作用。因为高斯分布在均值的位置采样概率最大,所以就忽略σ(z),让最后的 μ(z) 和 数据 x 越接近越好。
VAE 的问题就是不会生成新的数据,产生的数据是训练集中已有的、最多可能也只是训练集中已经有的数据的线性组合。这是被定义在 component 层面的目标函数所限制的。