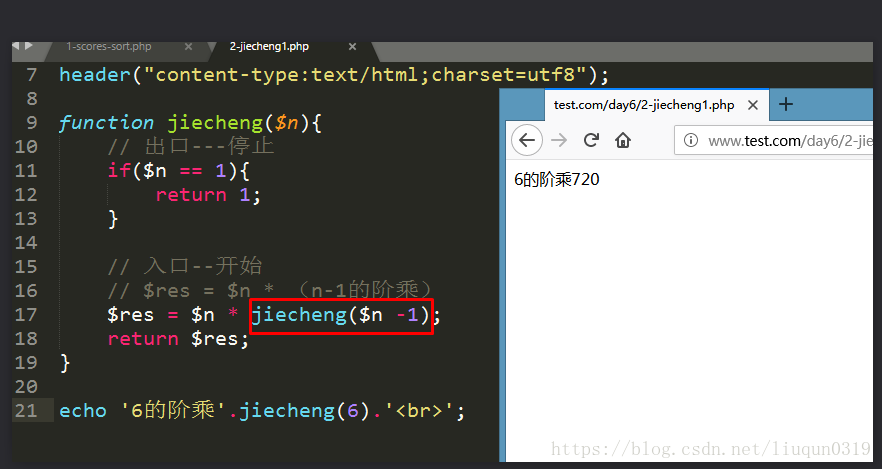
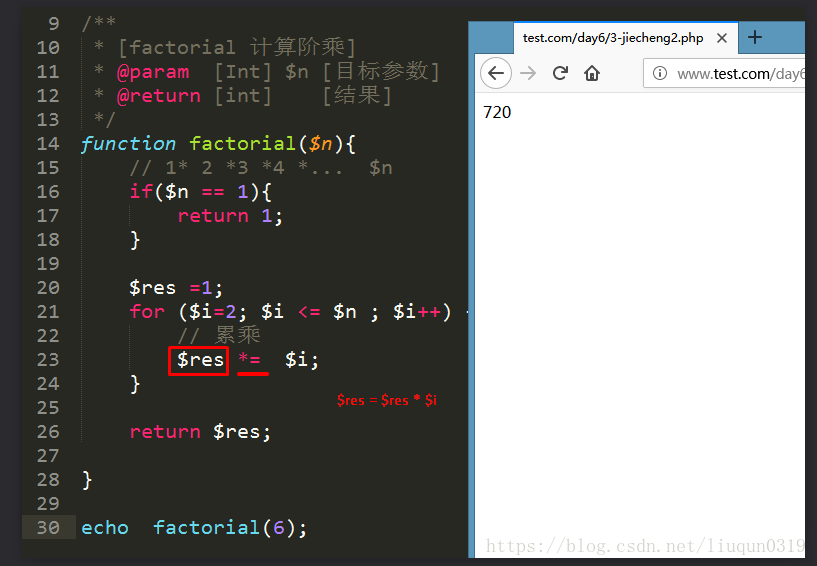
阶乘的求解思路:
5! = 5 * 4!
5! = 5 * 4 * 3!
5! = 5 * 4 * 3 * 2!
5! = 5 * 4 * 3 * 2 * 1!
1! =1;
计算5的阶乘时,没有立即计算出结果,需要求更低的阶乘
求5 的阶乘,核心:求其他数的阶乘。
定义一个求阶乘的函数fn: fn(5) = 5 * fn(4)
剩下的阶乘: fn($n )
在函数fn()中调用本身。
1)介绍
将大问题拆分成多个小问题来解决。
小问题的解决方法与大问题的解决方法一致。
可以封装函数来解决大问题(求阶乘的函数fn)
小问题的解决可以通过调用该函数来fn实现,只是输入的参数不一致而已。
2)本质
由于小问题的解决方法与大问题的解决方法一致,函数内部去调用函数本身。
3)递归两要素
递归的调用点(入口):什么情况下函数开始调用本身。f(5) = 5 * f(4)
递归的出口。什么时候结束递归调用的问题。对于阶乘来说:计算1的阶乘,
4)应用:阶乘
5)递归的执行原理
调用一次函数,不会理解得到结果。需要按照新参数执行函数。不断的调用新的函数,直到拿到确定的值,再返回,逐层拿到计算结果。执行时占用的空间比较大。
百数之和:
在1+ 2 + 3+ 4…
将上一次运算的结果作为条件,计算下一个的结果
7)介绍
又称递推:
将已知条件作为迭代的原始值,不断有原始值计算出新值的过程。执行效率非常高。
Fibanacci数列 :
一对兔子生小兔子的问题:
1 1 2 3 5 8 13 21 34
斐波那契额数列:有如下一个数列:1, 2, 3, 5, 8, 13, 21,……. 其规则是:前两个已知(即1和2),从第3个开始,其值为其左边两个值的和(此数列称为斐波那契数列)。定义一个函数,该函数可以求出该数列的任意第n个数的值。
function Fei( $n ){
if ( $n==1 ) { //特例值
return 1;
} else if ( $n==2 ) { //特例值
return 2;
} else {
return Fei($n-1) + Fei($n-2); //递归调用
}
}3.递归与递推的差异
递归在运行过程中不断开辟程序运行的内存空间,占用空间比较大。执行效率比较低。
但是在某些情况,如读取文件夹,由于不知道文件夹有多少层,此时只能使用递归思想。