一,定义
1.1 锐角三角函数
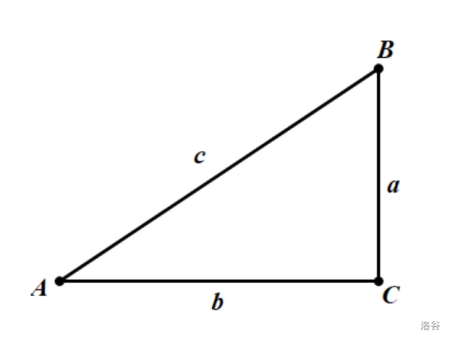
如图,在 ({ m Rt} riangle ABC) 中,(angle C=90^{circ}) ,则有:
(sin A=dfrac ac) (正弦值等于对边比斜边)
(cos A=dfrac bc) (余弦值等于邻边比斜边)
( an A=dfrac ab) (正切值等于对边比邻边)
(cot A=dfrac ba) (余切值等于邻边比对边)
(sec A=dfrac cb) (正割值等于斜边比邻边)
(csc A=dfrac ca) (余割值等于斜边比对边)
中学阶段最常用的是 (sin,cos, an,cot)
下文将不再讨论 (sec,csc) 及其他三角函数
1.2 任意角三角函数
构造平面直角坐标系 (xOy)
将 (x) 轴正半轴绕点 (O) 逆时针旋转一个角度 ( heta) 得到射线 (l)
设 (P(x,y)) 为 (l) 上一点,(OP=r) ,则有:
(sin heta=dfrac yr)
(cos heta=dfrac xr)
( an heta=dfrac yx)
(cot heta=dfrac xy)
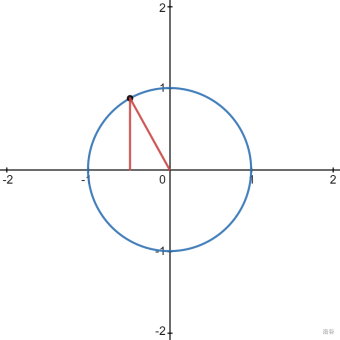
下图是 (alphain(frac{pi}2,pi)) 的情况
黑点为 (l) 与单位圆的交点,其横坐标即为 (cosalpha) ,纵坐标即为 (sinalpha)
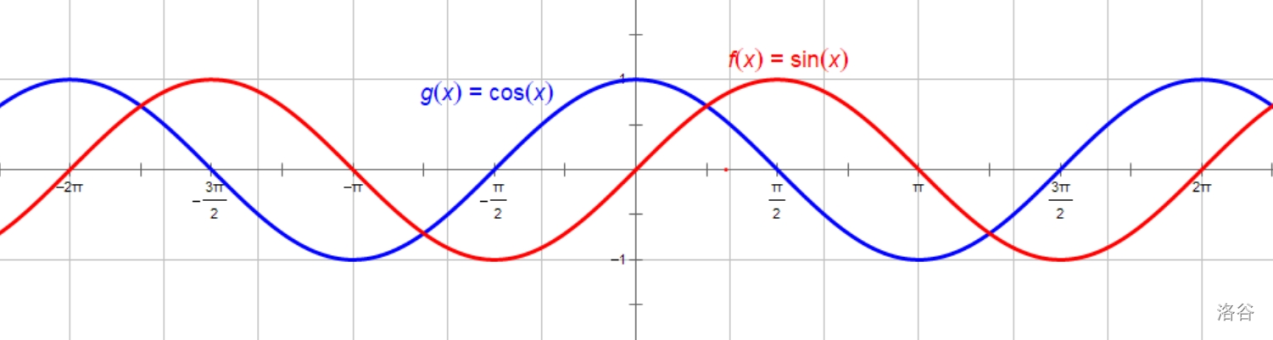
(sin) 和 (cos) 的函数图象如下图所示
1.3 反三角函数
反三角函数指三角函数的反函数,用 arc + 函数名 的形式表示
如 (arctandfrac ab) 表示满足 ( an heta=dfrac ab) 的 ( heta) 值
(arctan) 的值域(主值区间)为 ((-fracpi 2,fracpi 2)) ,这是为了保证一个自变量恰好对应一个函数值,同时方便使用
(arcsin,arccos,operatorname{arccot}) 的值域可参考 2.1 中表格
二,基本性质
2.1 定义域 & 值域
| 三角函数 | 定义域 | 值域 | 反三角函数 | 定义域 | 值域(主值区间) |
|---|---|---|---|---|---|
| (sin) | (mathbb R) | ([-1,1]) | (arcsin) | ([-1,1]) | ([-fracpi 2,fracpi 2]) |
| (cos) | (mathbb R) | ([-1,1]) | (arccos) | ([-1,1]) | ([0,pi]) |
| ( an) | ({xmid x e kpi+fracpi 2(kin mathbb Z)}) | (mathbb R) | (arctan) | (mathbb R) | ((-fracpi 2,fracpi 2)) |
| (cot) | ({xmid x e kpi(kin mathbb Z)}) | (mathbb R) | (operatorname{arccot}) | (mathbb R) | ((0,pi)) |
2.2 奇偶性 & 单调性 & 周期性
| 三角函数 | 奇偶性 | 最小正周期 | 反三角函数 | 奇偶性 | 单调性 |
|---|---|---|---|---|---|
| (sin) | 奇 | (2pi) | (arcsin) | 奇 | 单调递增 |
| (cos) | 偶 | (2pi) | (arccos) | 非奇非偶 | 单调递减 |
| ( an) | 奇 | (pi) | (arctan) | 奇 | 单调递增 |
| (cot) | 奇 | (pi) | (operatorname{arccot}) | 非奇非偶 | 单调递减 |
(sin,cos, an,cot) 的单调性请自行画图判断
(arcsin,arccos,arctan,operatorname{arccot}) 都不是周期函数
2.3 对称性
2.4 特殊值
| ( heta m(deg)) | (0^{circ}) | (30^{circ}) | (45^{circ}) | (60^{circ}) | (90^{circ}) | (120^{circ}) | (135^{circ}) | (150^{circ}) | (180^{circ}) |
|---|---|---|---|---|---|---|---|---|---|
| ( heta m(rad)) | (0) | (dfracpi6) | (dfracpi4) | (dfracpi3) | (dfracpi2) | (dfrac{2pi}3) | (dfrac{3pi}4) | (dfrac{5pi}6) | (pi) |
| (sin heta) | (0) | (dfrac12) | (dfrac{sqrt2}2) | (dfrac{sqrt3}2) | (1) | (dfrac{sqrt3}2) | (dfrac{sqrt2}2) | (dfrac12) | (0) |
| (cos heta) | (1) | (dfrac{sqrt3}2) | (dfrac{sqrt2}2) | (dfrac12) | (0) | (-dfrac12) | (-dfrac{sqrt2}2) | (-dfrac{sqrt3}2) | (-1) |
| ( an heta) | (0) | (dfrac{sqrt3}3) | (1) | (sqrt3) | (ackslash) | (-sqrt3) | (-1) | (-dfrac{sqrt3}3) | (0) |
| (cot heta) | (ackslash) | (sqrt3) | (1) | (dfrac{sqrt3}3) | (0) | (-dfrac{sqrt3}3) | (-1) | (-sqrt3) | (ackslash) |
(15^{circ}) 和 (75^{circ}) 的三角函数值也有可能会用到:
(sin15^{circ}=dfrac{sqrt6-sqrt2}4,~~cos15^{circ}=dfrac{sqrt6+sqrt2}4,~~ an15^{circ}=2-sqrt3,~~cot15^{circ}=2+sqrt3)
(sin75^{circ}=dfrac{sqrt6+sqrt2}4,~~cos75^{circ}=dfrac{sqrt6-sqrt2}4,~~ an75^{circ}=2+sqrt3,~~cot75^{circ}=2-sqrt3)
2.5 基本关系式
(sin^2 heta+cos^2 heta=1)
( an heta=dfrac{sin heta}{cos heta},~~cot heta=dfrac{cos heta}{sin heta})
( an hetacot heta=1)
(sin heta=cos(90^{circ}- heta),~~ an heta=cot(90^{circ}- heta))
证明略
三,三角恒等变形
3.1 诱导公式
诱导公式的作用是将 (ncdotdfracpi2pm alpha) 这种角的三角函数转化为 (alpha) 的三角函数
首先,根据三角函数的周期性,对于 ( heta=2kpi+alpha(kinmathbb Z)) ,有
(egin{aligned} sin(2kpi+alpha)&=sinalpha\ cos(2kpi+alpha)&=cosalpha\ an(2kpi+alpha)&= analpha\ cot(2kpi+alpha)&=cotalpha end{aligned})
诱导公式的其它部分如下表所示
| ( heta m(deg)) | (-alpha) | (90^{circ}-alpha) | (90^{circ}+alpha) | (180^{circ}-alpha) | (180^{circ}+alpha) | (270^{circ}-alpha) | (270^{circ}+alpha) | (360^{circ}-alpha) |
|---|---|---|---|---|---|---|---|---|
| ( heta m(rad)) | (-alpha) | (dfracpi2-alpha) | (dfracpi2+alpha) | (pi-alpha) | (pi+alpha) | (dfrac{3pi}2-alpha) | (dfrac{3pi}2+alpha) | (2pi-alpha) |
| (sin heta) | (-sinalpha) | (cosalpha) | (cosalpha) | (sinalpha) | (-sinalpha) | (-cosalpha) | (-cosalpha) | (-sinalpha) |
| (cos heta) | (cosalpha) | (sinalpha) | (-sinalpha) | (-cosalpha) | (-cosalpha) | (-sinalpha) | (sinalpha) | (cosalpha) |
| ( an heta) | (- analpha) | (cotalpha) | (-cotalpha) | (- analpha) | ( analpha) | (cotalpha) | (-cotalpha) | (- analpha) |
| (cot heta) | (-cotalpha) | ( analpha) | (- analpha) | (-cotalpha) | (cotalpha) | ( analpha) | (- analpha) | (-cotalpha) |
证明全部都可以直接套定义得到,但还是建议结合函数图象的性质理解记忆
3.2 和差角公式
(egin{aligned} sin(alpha+eta)&=sinalphacoseta+cosalphasineta\ sin(alpha-eta)&=sinalphacoseta-cosalphasineta\ cos(alpha+eta)&=cosalphacoseta-sinalphasineta\ cos(alpha-eta)&=cosalphacoseta+sinalphasineta\ an(alpha+eta)&=dfrac{ analpha+ aneta}{1- analpha aneta}\ an(alpha-eta)&=dfrac{ analpha- aneta}{1+ analpha aneta} end{aligned})
证明思路:
前四个中只需任意证明一个,再结合诱导公式即可得出另外三个
然后一三式、二四式分别相除即可得到五、六式
例如 ( an(alpha+eta)=dfrac{sin(alpha+eta)}{cos(alpha+eta)}=dfrac{sinalphacoseta+cosalphasineta}{cosalphacoseta-sinalphasineta})
分子分母同时约去 (cosalphacoseta) 即可得到 ( an(alpha+eta)=dfrac{ analpha+ aneta}{1- analpha aneta})
下面给出两种证明方法(在三角形内证明一式、向量法证明四式)
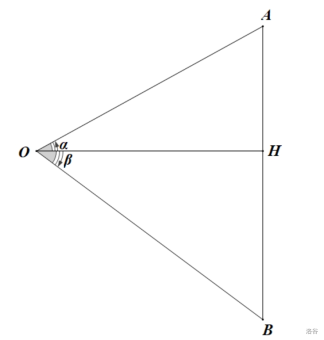
以 (alpha,eta) 均为锐角的情形为例
(S_{ riangle AOH}=dfrac12OAcdot OHcdot sinalpha=dfrac12OAcdot OBcdotcosetacdotsinalpha)
(S_{ riangle BOH}=dfrac12OBcdot OHcdot sineta=dfrac12OBcdot OAcdotcosalphacdotcoseta)
(S_{ riangle AOB}=dfrac12OAcdot OBcdot sin(alpha+eta))
显然 (S_{ riangle AOB}=S_{ riangle AOH}+S_{ riangle BOH}) ,故 (sin(alpha+eta)=sinalphacoseta+cosalphasineta) ,即为一式
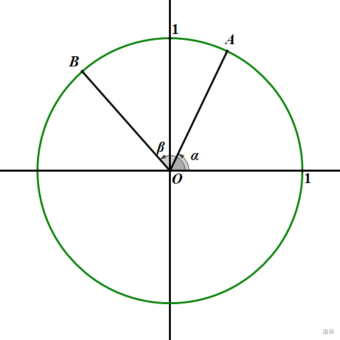
(A,B) 都在单位圆上,故 (A,B) 的坐标分别为 ((cosalpha,sinalpha),(coseta,sineta))
考虑向量 (overrightarrow{OA},overrightarrow{OB}) 的数量积
根据定义, (overrightarrow{OA}cdotoverrightarrow{OB}=|OA|cdot|OB|cdotcos(eta-alpha)=cos(eta-alpha)=cos(alpha-eta))
再考虑数量积的坐标表示,有 (overrightarrow{OA}cdotoverrightarrow{OB}=cosalphacoseta+sinalphasineta)
故 (cos(alpha-eta)=cosalphacoseta+sinalphasineta) ,即为四式
3.3 倍角公式
在和角公式中令 (alpha=eta) ,即可得到二倍角公式:
(egin{aligned} sin2alpha&=2sinalphacosalpha\ cos2alpha&=cos^2alpha-sin^2alpha=2cos^2alpha-1=1-2sin^2alpha\ an2alpha&=dfrac{2 analpha}{1- an^2alpha} end{aligned})
由二倍角公式可得 (cosalpha=2cos^2dfracalpha2-1=1-2sin^2dfracalpha2)
进一步可以推出半角公式:
(egin{aligned} sindfracalpha2&=pmsqrt{dfrac{1-cosalpha}2}\ cosdfracalpha2&=pmsqrt{dfrac{1+cosalpha}2}\ andfracalpha2&=pmsqrt{dfrac{1-cosalpha}{1+cosalpha}}=dfrac{sinalpha}{1+cosalpha}=dfrac{1-cosalpha}{sinalpha} end{aligned})
带 (pm) 是因为开方导致符号不确定,还需要根据 (dfracalpha2) 所在的象限判断
但 ( andfracalpha2=dfrac{sinalpha}{1+cosalpha}=dfrac{1-cosalpha}{sinalpha}) 是没有符号问题的 可以直接用
三倍角公式偶尔也会用到 但部分推导过程要用到和差化积/积化和差公式 所以放到后面再讲
四倍及以上就没必要记了
3.4 万能公式
功能是仅用 ( andfracalpha2) 表示出 (alpha) 的三角函数值
首先根据二倍角公式有
(egin{aligned} sinalpha&=2sindfracalpha2cosdfracalpha2\ cosalpha&=cos^2dfracalpha2-sin^2dfracalpha2\ analpha&=dfrac{2 anfracalpha2}{1- an^2fracalpha2} end{aligned})
三式已经达成目标了
因为 (1=sin^2fracalpha2+cos^2fracalpha2) ,所以我们可以把一二式写成
(sinalpha=dfrac{2sinfracalpha2cosfracalpha2}{sin^2fracalpha2+cos^2fracalpha2}, cosalpha=dfrac{cos^2fracalpha2-sin^2fracalpha2}{sin^2fracalpha2+cos^2fracalpha2})
然后就可以约分了,最终得到
(egin{aligned} sinalpha&=dfrac{2 anfracalpha2}{1+ an^2fracalpha2}\ cosalpha&=dfrac{1- an^2fracalpha2}{1+ an^2fracalpha2}\ analpha&=dfrac{2 anfracalpha2}{1- an^2fracalpha2} end{aligned})
即为万能公式
3.6 积化和差公式
根据和差角公式,(cos(alphapmeta)=cosalphacosetampsinalphasineta)
两式相加,两式相减,分别可得出
(egin{aligned} cosalphacoseta&=dfrac12[cos(alpha+eta)+cos(alpha-eta)]\ sinalphasineta&=dfrac12[cos(alpha-eta)-cos(alpha+eta)] end{aligned})
同理,由 (sin(alphapmeta)=sinalphacosetapmcosalphasineta) 可得
(egin{aligned} sinalphacoseta&=dfrac12[sin(alpha+eta)+sin(alpha-eta)]\ cosalphasineta&=dfrac12[sin(alpha+eta)-sin(alpha+eta)] end{aligned})
这四个式子就是积化和差公式
(egin{aligned} sinalphasineta&=-dfrac12[cos(alpha+eta)-cos(alpha-eta)]\ sinalphacoseta&=dfrac12[sin(alpha+eta)+sin(alpha-eta)]\ cosalphasineta&=dfrac12[sin(alpha+eta)-sin(alpha-eta)]\ cosalphacoseta&=dfrac12[cos(alpha+eta)+cos(alpha-eta)] end{aligned})
3.8 和差化积公式
(egin{aligned} sinalpha+sineta&=2sin frac{alpha+eta}2cos frac{alpha-eta}2\ sinalpha-sineta&=2cos frac{alpha+eta}2sin frac{alpha-eta}2\ cosalpha+coseta&=2cos frac{alpha+eta}2cos frac{alpha-eta}2\ cosalpha-coseta&=2cos frac{alpha+eta}2sin frac{alpha-eta}2 end{aligned})
证明不写了,用积化和差从右往左推就行
3.9 其它公式
三倍角公式
对二倍角和一倍角用一次和角公式即可
化简整理会用到和差化积/积化和差 不详细写了
(egin{aligned} sin3alpha&=3sinalpha-4sin^3alpha=4sin(60^{circ}-alpha)sinalphasin(60^{circ}+alpha) \ cos3alpha&=4cos^3alpha-3cosalpha=4cos(60^{circ}-alpha)cosalphacos(60^{circ}+alpha) \ an3alpha&=dfrac{ an^3alpha-3 analpha}{3 an^2alpha-1}= an(60^{circ}-alpha) analpha an(60^{circ}+alpha) end{aligned})
辅助角公式
(asin x+bcos x=sqrt{a^2+b^2}sin(x+arctanfrac ba))
用和角公式把右边拆了就能证
可以用来处理最值问题