(一)什么是多项式回归
还记得线性回归法吗?线性回归法有一个很大的局限性,那就是需要数据是有一定的线性关系的,但是现实中的很多数据是没有线性关系的。多项式就是用来解决这个问题的,可以处理非线性数据
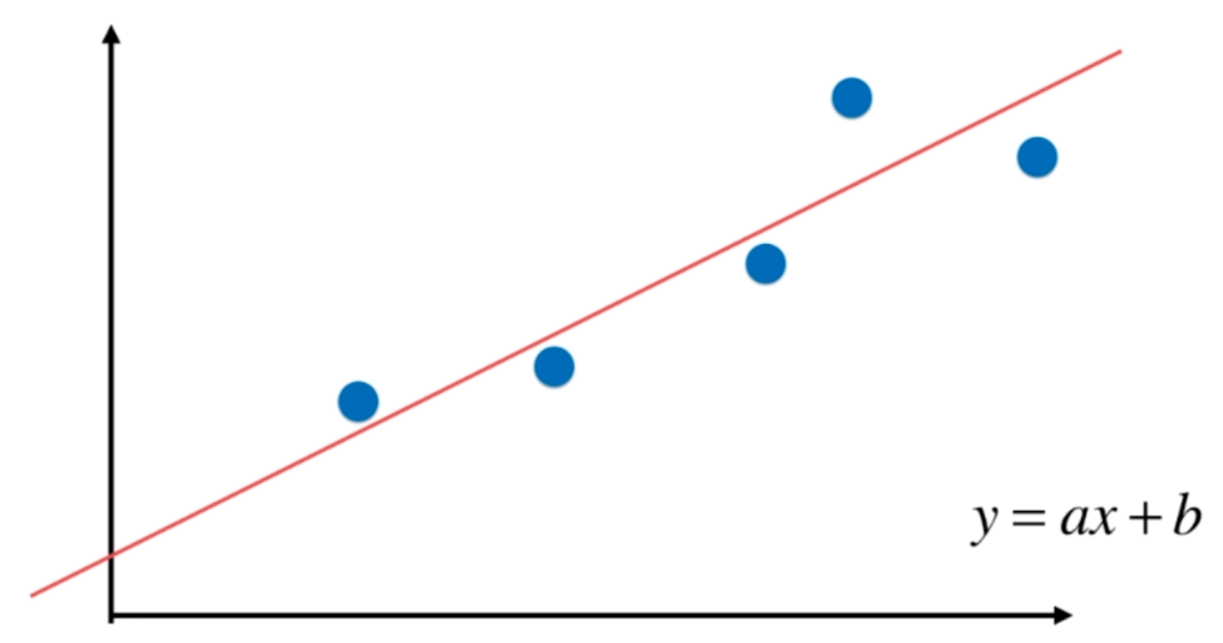
在线性回归中,我们是假设数据具有线性关系的,因此我们在简单线性回归中,将直线的方向设置为y=ax+b的形式,那么我们求出a和b即可。
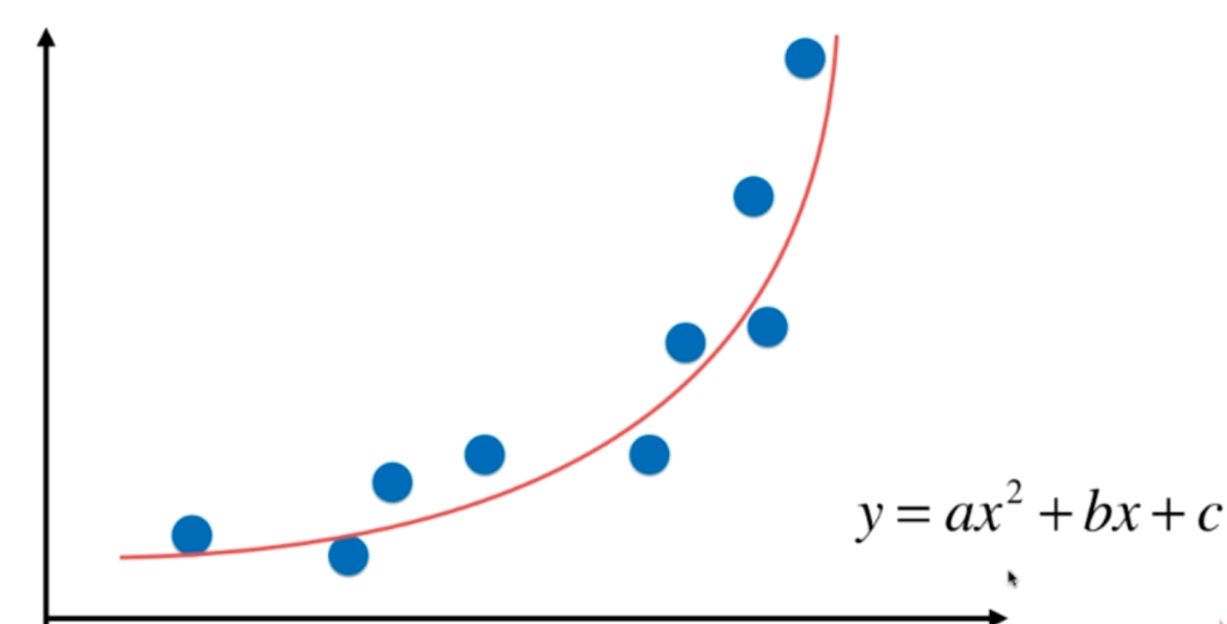
而对于有些数据,我们虽然也可以使用线性回归,但是显然具有更加强的非线性的关系,换句话说,如果我们用一个二次曲线来拟合这些点,效果会更好。因此函数就变成了了y=ax^2+bx+c,我们求出a、b、c即可。但是本质上,和线性回归一样,目前都是只有一个特征,只不过我们为样本多添加了一些特征,这些特征是原来的多项式项。求出了对原来的特征而言,一个非线性的曲线。
生成数据集
import numpy as np
import matplotlib.pyplot as plt
# 生成一百个样本,每个样本只有一个特征
X = np.random.uniform(-3, 3, size=(100, 1))
y = 0.5 * X ** 2 + X + 2 + np.random.normal(0, 1, size=(100,1))
plt.scatter(X, y)
plt.show()
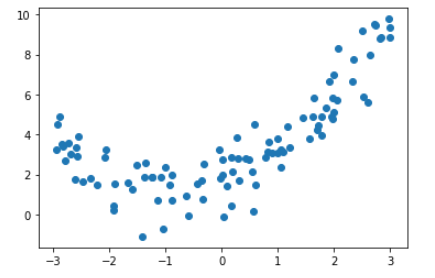
可以看到数据大概满足一条二次曲线,但是我们使用线性回归法来拟合一下
from sklearn.linear_model import LinearRegression
linear = LinearRegression()
linear.fit(X, y)
y_predict = linear.predict(X)
plt.plot(X, y_predict, color="red")
plt.scatter(X, y)
plt.show()
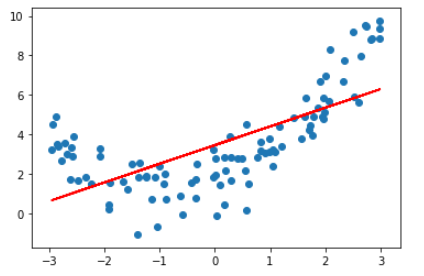
显然这种拟合效果是不够好的,我们来给样本添加一个平方项。
from sklearn.linear_model import LinearRegression
X2 = np.c_[X ** 2, X]
linear2 = LinearRegression()
linear2.fit(X2, y)
y_predict2 = linear.predict(X2)
plt.plot(np.sort(X, axis=0), y_predict2[np.argsort(X, axis=0)].flat, color="red")
plt.scatter(X, y)
plt.show()
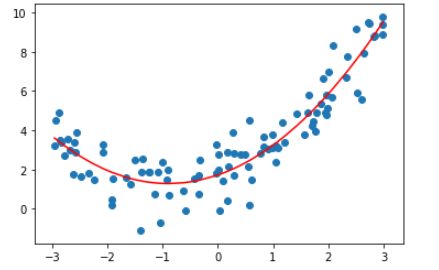
我们来看看系数
print(linear2.coef_) # [[0.54629821 0.97561867]]
print(linear2.intercept_) # [1.71831689]
可以发现预测的还算是蛮准确的,与此同时我们发现这有点像反过来的pca啊,一种升维的思想。
(二)sklearn中的多项式回归与pipline
import numpy as np
import matplotlib.pyplot as plt
X = np.random.uniform(-3, 3, size=(100, 1))
y = 0.5 * X ** 2 + X + 2 + np.random.normal(0, 1, size=(100,1))
# 值得一提的是,多项式回归在sklearn中被封装到了preprocessing模块下
# 这是因为我们在使用线性回归的时候,是不是给原来的样本多添加了一个特征
# 因此这可以看成是预处理,所以被封装到了preprocessing木块下
from sklearn.preprocessing import PolynomialFeatures
# degree这个参数表示要为原来的x添加几次幂
poly = PolynomialFeatures(degree=2)
X2 = poly.fit_transform(X)
print(X2[: 5])
"""
[[ 1. 1.43606298 2.06227689]
[ 1. 0.06661937 0.00443814]
[ 1. 1.48962145 2.21897206]
[ 1. 2.05925905 4.24054782]
[ 1. -1.60056297 2.56180181]]
"""
# 我们发现fit_transform之后,列数增加了一列
# 相当于帮我们增加了一个X的0次幂,第二列是X的1次幂,第三列是X的2次幂
# 而第二列就是原本的X
from sklearn.linear_model import LinearRegression
linear = LinearRegression()
linear.fit(X2, y)
y_predict = linear.predict(X2)
plt.scatter(X, y)
plt.plot(np.sort(X, axis=0), y_predict[np.argsort(X,axis=0).flat],color="red")
plt.show()
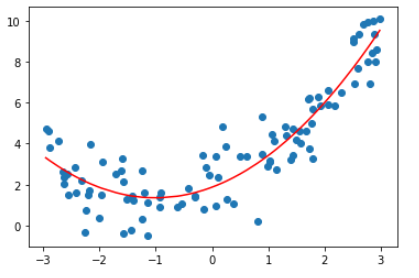
print(linear.coef_) # [[0. 1.03279553 0.51398532]]
print(linear.intercept_) # [1.87408764]
关于PolynomialFeatures,我们再来探讨一下
import numpy as np
from sklearn.preprocessing import PolynomialFeatures
X = np.arange(1, 11).reshape((-1, 2))
poly = PolynomialFeatures(degree=2)
X2 = poly.fit_transform(X)
print(X)
"""
[[ 1 2]
[ 3 4]
[ 5 6]
[ 7 8]
[ 9 10]]
"""
print(X2)
"""
[[ 1. 1. 2. 1. 2. 4.]
[ 1. 3. 4. 9. 12. 16.]
[ 1. 5. 6. 25. 30. 36.]
[ 1. 7. 8. 49. 56. 64.]
[ 1. 9. 10. 81. 90. 100.]]
"""
可以看到,原本5行2列的数据,在经过多项式回归转化之后,变成了5行6列的数据。第一列是X的零次幂,第二列和第三列是原来的样本。第四列是原来样本第一列的平方,第五列是原来样本的第一列乘上第二列,第六列是原来样本的第二列的平方。因此当degree=2的时候,2次项会增加三列。
同理degree=3的时候,会考虑所有的3次方,2次方,1次方,0次方。表现如下
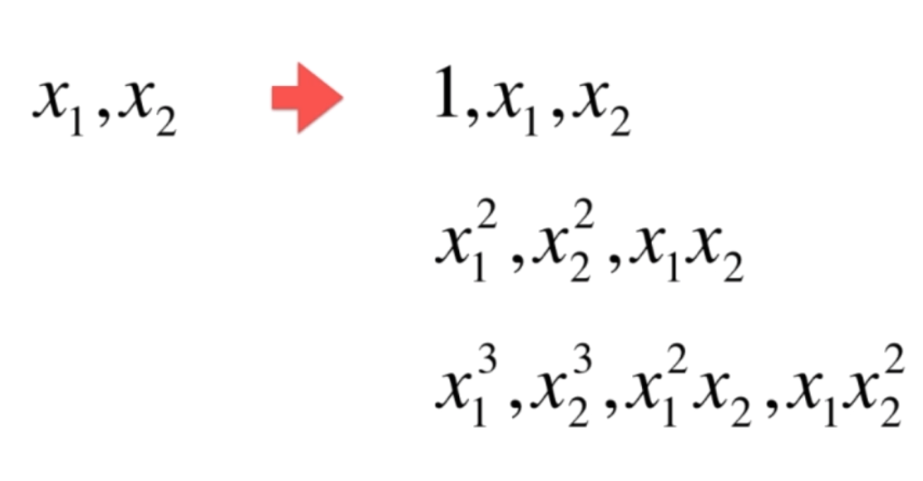
pipeline
pipeline是一个管道,可以将一系列操作组合起来。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler, PolynomialFeatures
from sklearn.linear_model import LinearRegression
# 将每一个步骤随便起一个名字
# 然后以列表的形式放到Pipeline里面
pip_reg = Pipeline([
("多项式", PolynomialFeatures(degree=2)),
("数据标准化", StandardScaler()),
("线性回归", LinearRegression())
])
# 此时我调用Pipeline的实例,传入数据
# 那么数据会按照管子里面定义的三个操作的顺序,依次执行
X = np.random.uniform(-3, 3, size=(100, 1))
y = 0.5 * X ** 2 + X + 2 + np.random.normal(0, 1, (100, 1))
# 调用方式还是使用fit
# 会非常智能的将X先经过PolynomialFeatures处理得到新的X
# 再将新的X交给StandardScaler处理得到再一个新的X
# 然后将最终处理的全新的X和y交给LinearRegression
pip_reg.fit(X, y)
y_predict = pip_reg.predict(X)
plt.scatter(X, y)
plt.plot(np.sort(X, axis=0), y_predict[np.argsort(X, axis=0).flat], color="red")
plt.show()
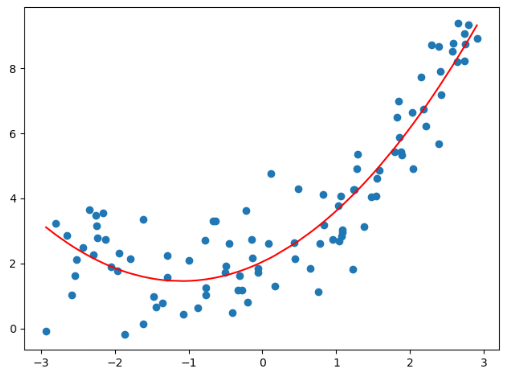
得到的结果依旧是准确的,而且使用更加方便了。
(三)过拟合与欠拟合
通过多项式回归,我们可以轻松的对非线性数据进行拟合,但是过度的使用也会带来一个问题。我们实际演示一下
import numpy as np
import matplotlib.pyplot as plt
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler, PolynomialFeatures
from sklearn.linear_model import LinearRegression
# 可以看到,我们自己封装了一个多项式回归
# 因为在sklearn中并没有直接对多项式回归封装成一个类
def PolynomialRegression(degree):
return Pipeline([
("多项式", PolynomialFeatures(degree)),
("数据标准化", StandardScaler()),
("线性回归", LinearRegression())
])
X = np.random.uniform(-3, 3, size=(100, 1))
y = 0.5 * X ** 2 + X + 2 + np.random.normal(0, 1, (100, 1))
poly = PolynomialRegression(200)
poly.fit(X, y)
y_predict = poly.predict(X)
plt.scatter(X, y)
plt.plot(np.sort(X, axis=0), y_predict[np.argsort(X, axis=0).flat], color="red")
plt.show()
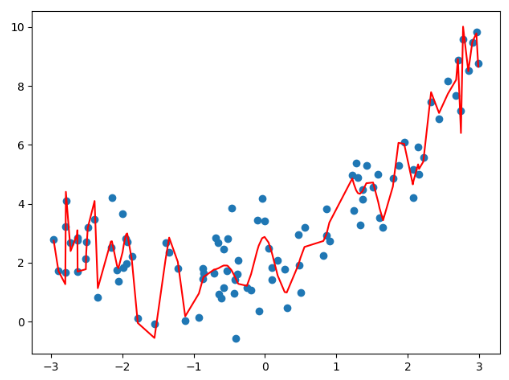
很明显,当我们degree=200的时候,拟合效果比原来更好了,其实也很好理解,随着degree的增大,我们总能找到一根曲线来拟合所以的样本点,使得整体的均方误差为0。不过这里产生了一个疑问,虽然在训练集上拟合样本点拟合的很好,但是这真的是一根描述样本走向的曲线吗?我们可以观察一下图像,有的样本点在x轴上明明距离很近,但是它们的预测值却相差很远。换句话说,只是为了单纯的拟合这些点,尽管在训练集上表现的很好,但是在预测集上面的效果一定会很差。因此这就是所谓的过拟合(over-fitting)现象,为了拟合所有的数据,从而丢失了数据整体的走向。那么同理对于一开始的线性回归,又有很多的样本点拟合不上,这便是所谓的欠拟合(under-fitting)现象
(四)为什么需要训练集和测试集
模型的泛化能力
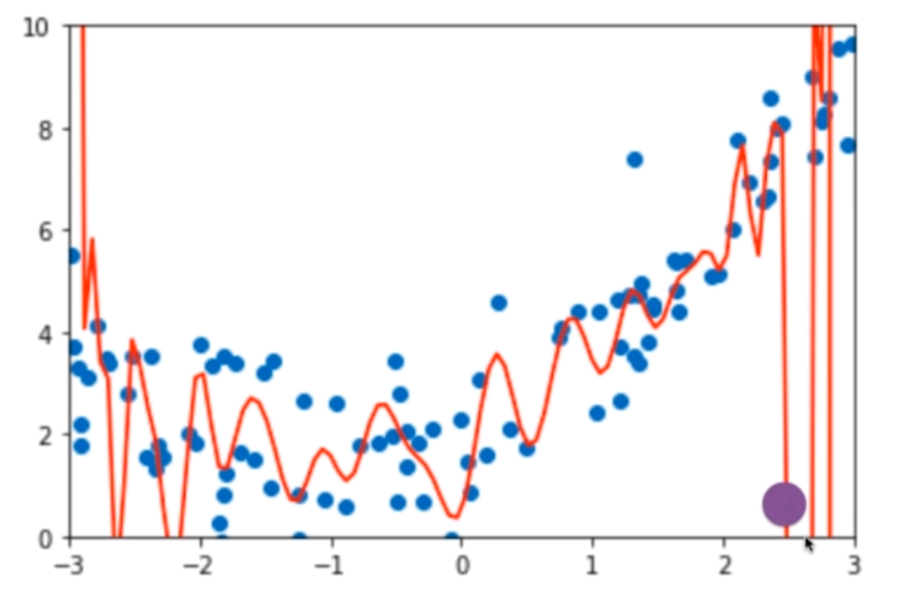
我们来看一下这个紫色的点,发现它和原来的蓝色的点不在同一趋势上,虽然我们原来的蓝色样本点拟合的很好,但是当来一个新的样本的时候,就完蛋了,预测的结果非常的差,那么我们就说这个模型的泛化能力非常的差,泛化能力就是在训练集上面的表现的很好,但是来新的样本的时候,所表现的能力就变差了,这便是过拟合所带来的的后遗症。我们在训练集上面表现的有多好,其实是没有意义的,我们关注的是这个模型的泛化能力有多好。所以我们才要有训练集和测试集,在训练集上面只是训练模型,我们关注的是在测试集上面,也就是新的样本,它的泛化能力、预测能力、或者说预测结果能有多好。
我们来将数据集分为训练集和测试集,用训练集训练,测试集预测score。看看不同的degree对score的影响
import numpy as np
import matplotlib.pyplot as plt
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler, PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
# 可以看到,我们自己封装了一个多项式回归
# 因为在sklearn中并没有直接对多项式回归封装成一个类
def PolynomialRegression(degree):
return Pipeline([
("多项式", PolynomialFeatures(degree)),
("数据标准化", StandardScaler()),
("线性回归", LinearRegression())
])
X = np.random.uniform(-3, 3, size=(100, 1))
y = 0.5 * X ** 2 + X + 2 + np.random.normal(0, 1, (100, 1))
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
for i in [2, 20, 50, 100, 200]:
poly = PolynomialRegression(i)
poly.fit(X_train, y_train)
print(f"degree={i} score={poly.score(X_test, y_test)}")
"""
degree=2 score=0.8944854282792039
degree=20 score=0.6084274531096586
degree=50 score=-346373289947.1378
degree=100 score=-3.851130500643901e+19
degree=200 score=-1.0215530446065044e+26
"""
可以看到degree=2的时候,是0.89,degree=20是0.60,再之后就惨不忍睹了,score都为负数、而且负的都没边了,说明模型的泛化能力太差了,可以看到尽管degree增大在训练集上拟合的很好,但是在测试集上很糟糕,这不是我们想要的。
所以模型的复杂度和模型预测的准确率在训练集和测试集上分别有如下关系
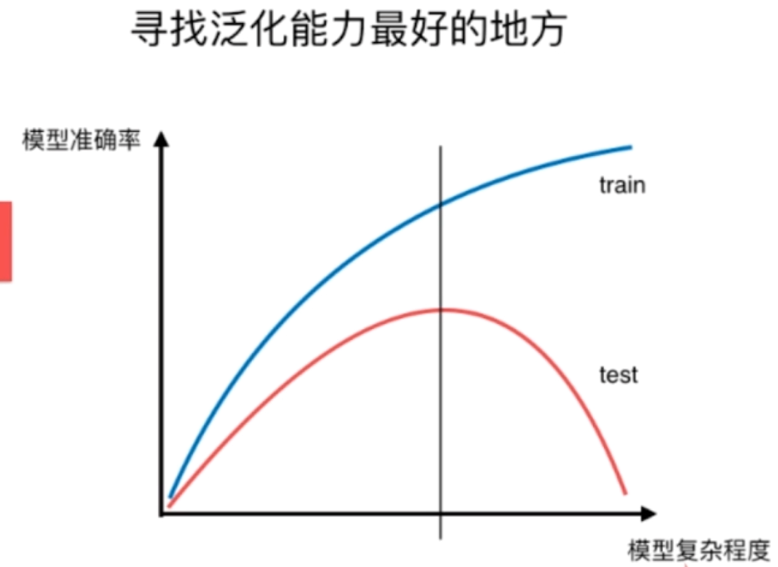
对于训练集很好理解,对于测试集则是类似于一个开口向下的二次函数,从左往右依次经历欠拟合,到中间达到正合适,到右边过拟合。
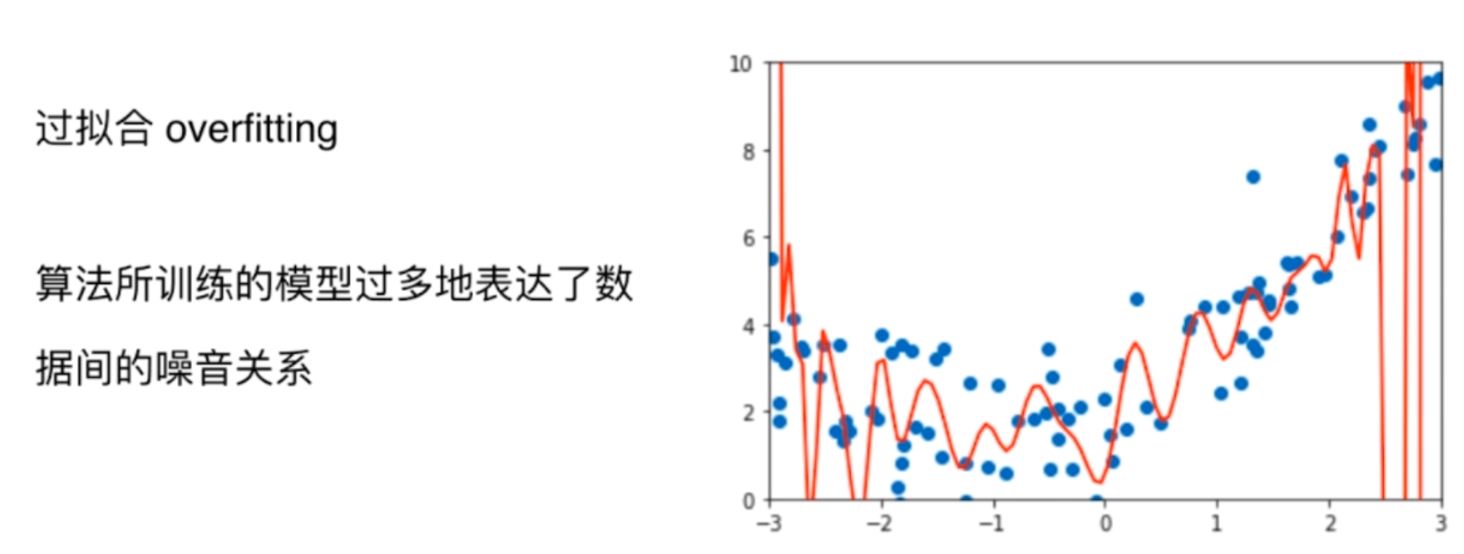
(五)学习曲线
学习曲线就是随着训练样本的逐渐增多,算法训练出的模型所表现除的能力。下面我们来实际操作一下
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
X = np.random.uniform(-3, 3, size=(100, 1))
y = 0.5 * X ** 2 + X + 2 + np.random.normal(0, 1, (100, 1))
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
train_score = []
test_score = []
# 我们的训练样本数从小到大一次递增,我们看看训练的效果如何
for i in range(1, X_train.shape[0] + 1):
lin_reg = LinearRegression()
# 每次只用前i个样本训练
lin_reg.fit(X_train[: i], y_train[: i])
# 预测前i个样本
y_train_predict = lin_reg.predict(X_train[: i])
train_score.append(np.sqrt(mean_squared_error(y_train[: i], y_train_predict)))
y_test_predict = lin_reg.predict(y_test)
test_score.append(np.sqrt(mean_squared_error(y_test, y_test_predict)))
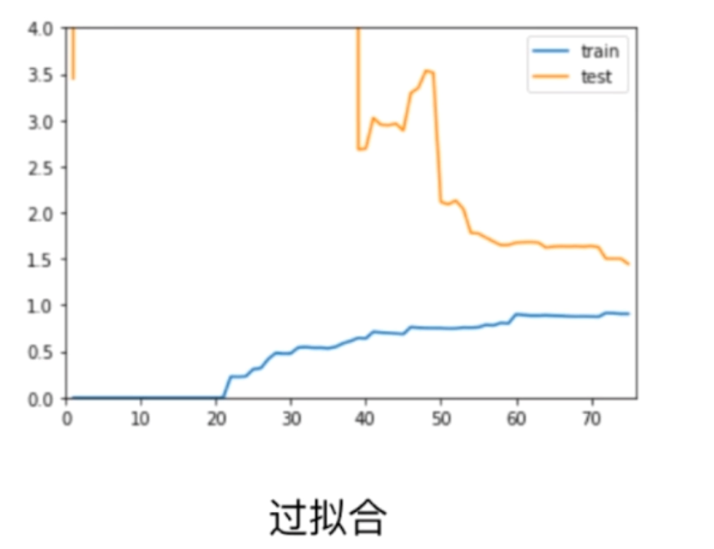
plt.plot(list(range(1, X_train.shape[0] + 1)), train_score, label="train")
plt.plot(list(range(1, X_train.shape[0] + 1)), test_score, label="test")
plt.legend()
plt.grid()
plt.show()
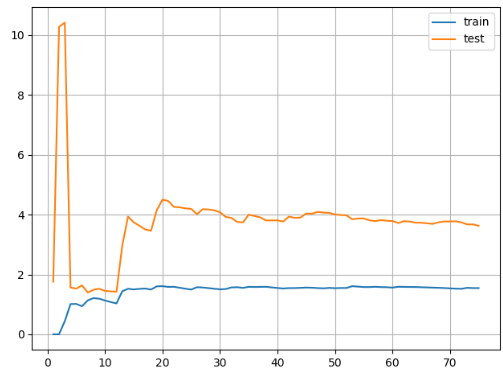
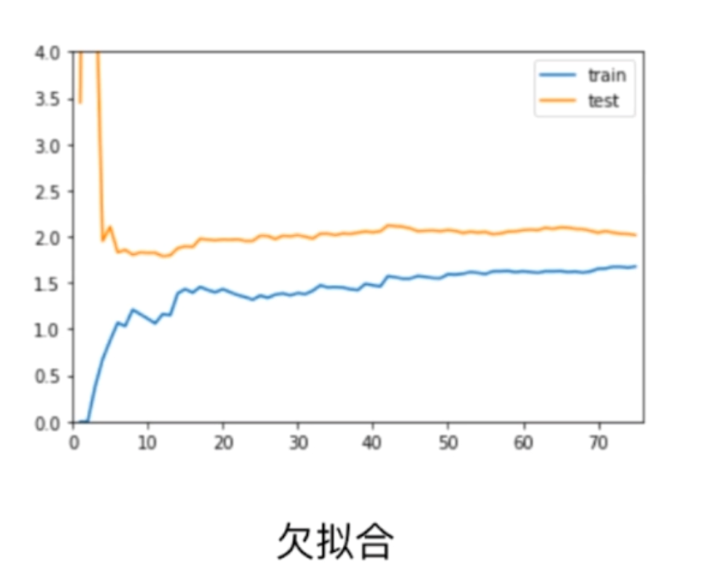
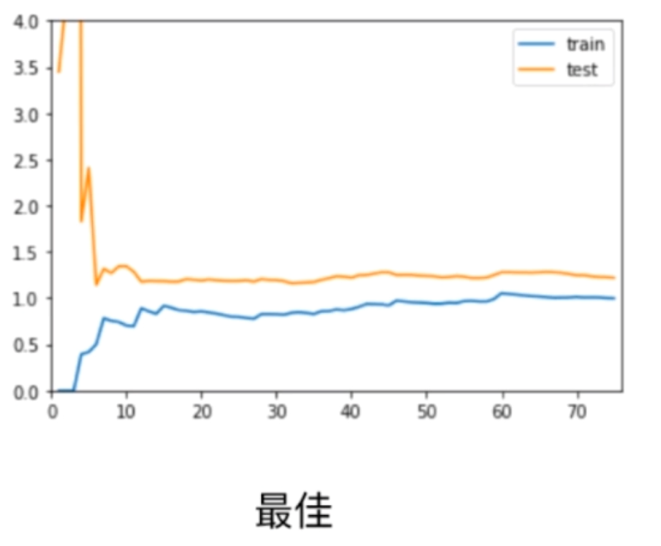
对于训练集来说,由于一开始样本较少,整体误差较少,但是随着样本增大,误差增大,但是最终会稳定在一个值附近。而对于测试集来说,由于训练的就是全部的测试集,训练样本较少,拟合的程度较差,因此一开始会增大,但是最终也会稳定在一个值附近。而测试集需要考验模型一定的泛化能力,最终测试集的误差较大一些,这也是合理的。
(六)验证数据集与交叉验证
测试数据集的意义
如果我们把全部的数据集都当做训练集,那么容易发生了过拟合而我们却不自知。因此我们需要把数据集分成训练集和测试集,那么我们使用训练集训练的模型,可以使用测试集进行检验,通过测试集来判断模型的好坏。如果在测试集上表现的很好的话,那么说明模型的泛化能力强,那么在面对未知的数据时能有更好的表现。
但是这样也会有一个问题,那就是当我们的模型在测试集上表现不好的时候,我们就会重新调整参数、重新训练,说明我们的模型一直在围绕着测试集打转,目的就是使得模型在测试集上表现的效果最好。但是由于测试数据集是已知的,说明我们的模型一直在针对测试数据集进行调参。那么这也有可能产生过拟合的可能,也就是我们的模型对测试集数据产生了过拟合。
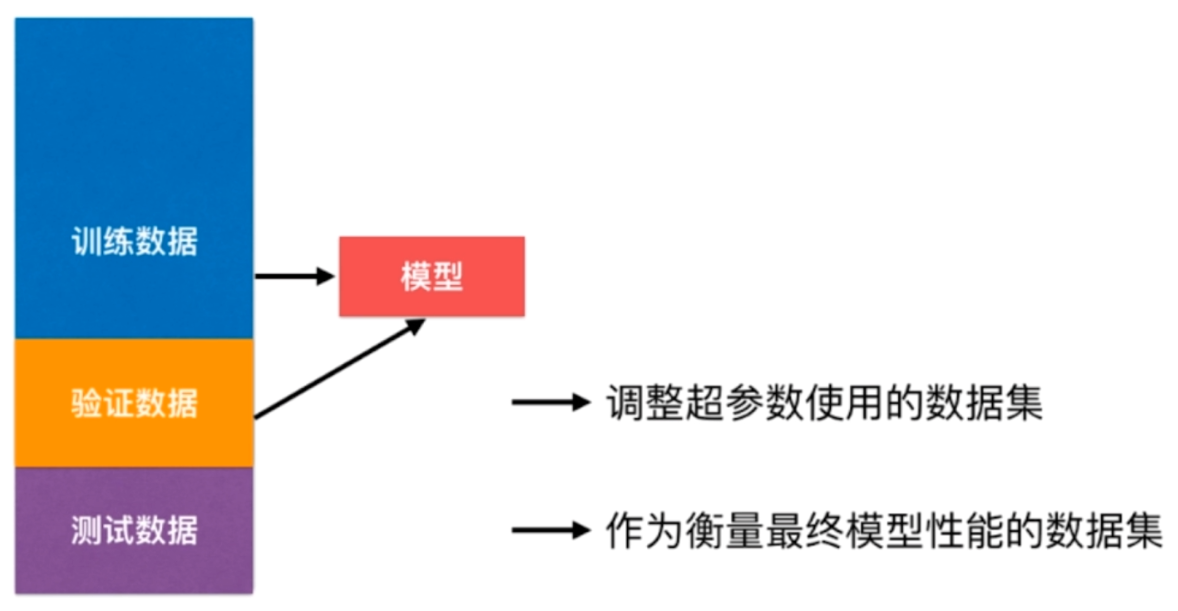
那么如何才能解决这个问题呢?那就是我们可以将数据集分成三部分,训练数据集、验证数据集、测试数据集,首先训练数据集不必说,验证数据集做的就是之前的测试数据集所做的事情,如果效果不好,那么我们就要重新调整参数,最后第三部分,测试数据集作为衡量模型最终性能的数据集
因此此时的测试集是不参与模型的训练的,训练集用于训练模型,验证集用于验证模型的好坏,如果不行,就重新训练,这都叫参与模型的训练。而对于测试集来说,模型是完全不可知的,只是单纯的作为衡量模型的性能的最终手段
但是这样还有一个问题,目前我们只有验证数据集这一份,如果当中出现了极端数据的话怎么办呢?因此为了解决这个问题,就有了交叉验证(cross validation)
交叉验证(cross validation)
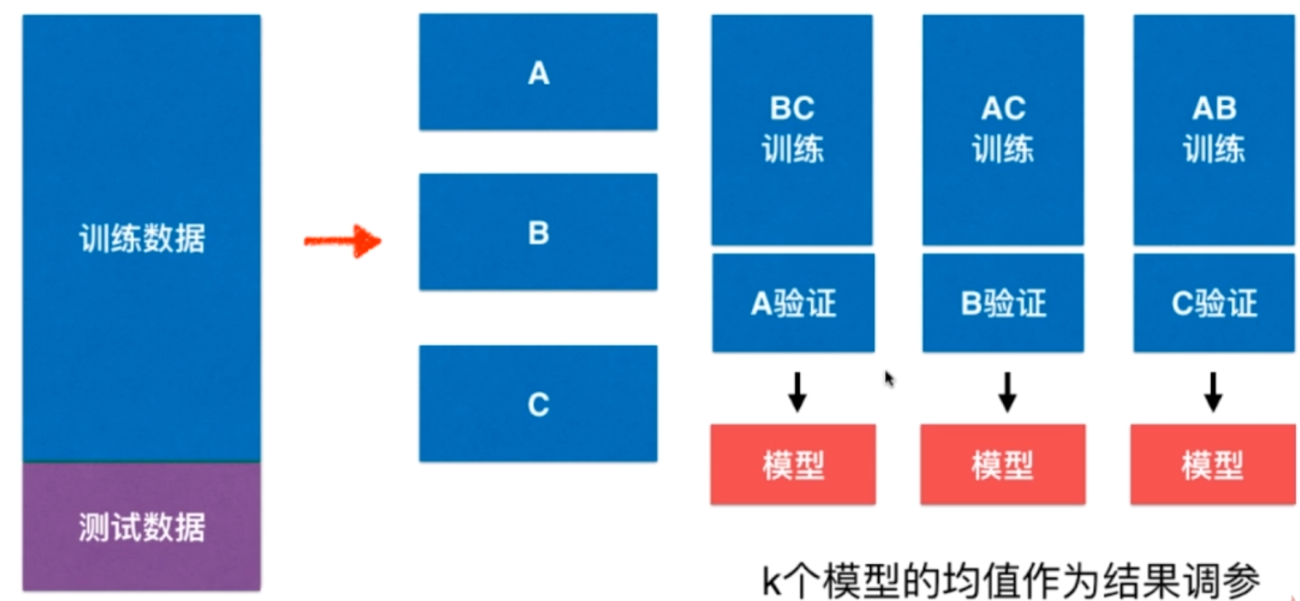
我们将训练数据集分成k份,比如这里分成3份,当BC作为训练集的时候,A作为验证集;AC作为训练集,B作为验证集;AB作为训练集,C作为验证集。如果分成K份,那么显然会产生K个模型,我们使用K个模型的均值作为结果进行调参,这样就可以避免极端数据所带来的影响。这就是交叉验证
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.datasets import load_digits
digit = load_digits()
X = digit.data
y = digit.target
X_train, X_test, y_train, y_test = train_test_split(X, y)
# 参数是我提前取好的
knn_clf = KNeighborsClassifier(n_neighbors=4, p=3, weights="distance")
print(cross_val_score(knn_clf, X_train, y_train)) # [0.98447894 0.98666667 0.99103139]
"""
可以看到sklearn中的交叉验证,自动帮我们分成了三组。
但是在0.22版本中,将会自动分成五组
"""
首先我们两层for循环,肯定能找到一个比较好的k和p,但是这有可能存在极端情况,下面我们使用交叉验证来看看
import numpy as np
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.datasets import load_digits
digit = load_digits()
X = digit.data
y = digit.target
X_train, X_test, y_train, y_test = train_test_split(X, y)
best_k, best_p, best_score = 0, 0, 0
for k in range(2, 11):
for p in range(1, 6):
knn_clf = KNeighborsClassifier(n_neighbors=k, p=p, weights="distance")
scores = cross_val_score(knn_clf, X_train, y_train)
score = np.mean(scores)
if score > best_score:
best_k, best_p, best_score = k, p, score
print(f"k={best_k},p={best_p}, score={best_score}") # k=2,p=2, score=0.9895696014200538
"""
我们之前k取4,p取3,没有使用交叉验证,而是普通的预测分数得出来的结果。
而现在使用交叉验证,得到结果是k=2,p=2,我们更应该相信使用交叉验证得出来的结果。
"""
回顾一下网格搜索,sklearn的网格搜索也是使用了交叉验证的手段,在k近邻当中我们就使用了。
import numpy as np
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV
from sklearn.datasets import load_digits
digit = load_digits()
X = digit.data
y = digit.target
X_train, X_test, y_train, y_test = train_test_split(X, y)
knn_clf = KNeighborsClassifier()
params = [
{
"weights": ["distance"],
"n_neighbors": list(range(2, 11)),
"p": list(range(1, 6))
}
]
grid_search = GridSearchCV(knn_clf, params)
grid_search.fit(X_train, y_train)
print(grid_search.best_params_) # {'n_neighbors': 2, 'p': 3, 'weights': 'distance'}
print(grid_search.best_score_) # 0.9844097995545658
由于我是在pycharm中执行的,train_test_split所分割的样本是随机的,导致得出来的参数略有不同
以上面试交叉验证,如果我们想每一次多分几份,比如5份,那么只需要在cross_val_score中指定cv=5即可,同理在GridSearchCV当中也是一样的。
我们把训练集分成k份,称之为K-folds cross validation,每一份都可以成为一个fold,每一次拿出k-1份当成训练集,剩余的一份当成测试集。但是这有一个缺点,那就是每一次要训练k个模型,也意味着性能慢了K倍
在极端情况下,我们也可以使用留一法(LOO-CV)这种交叉验证的模式。留一法可以看成是KFold的一个特例。我们说KFold是将m个样本分成k份,每次选k-1份训练,然后剩余的那一份预测。而留一法则是如果有m个样本,那么就把数据集分成m份(等于KFold中的k取整个样本数:m),然后每次训练m-1份,然后看剩余的那一份样本准不准,这样的话就完全不受随机的影响,是最近模型真正的性能指标。想象K-folds,虽然分成了K份,但是这K份怎么分,也会带来一定的影响,而留一法(leave-one-out cross validation)则完全不受随机带来的影响。但是也有缺点,那就是运算量巨大(样本如果有100万个,那么要训练100万个模型)。如果计算资源不是很富裕的话,一般很少采用这种交叉验证的模式。但是在学术上,为了严谨性,最后可能会采用这种交叉验证的方式。
(七)偏差方差权衡
什么是偏差和方差?
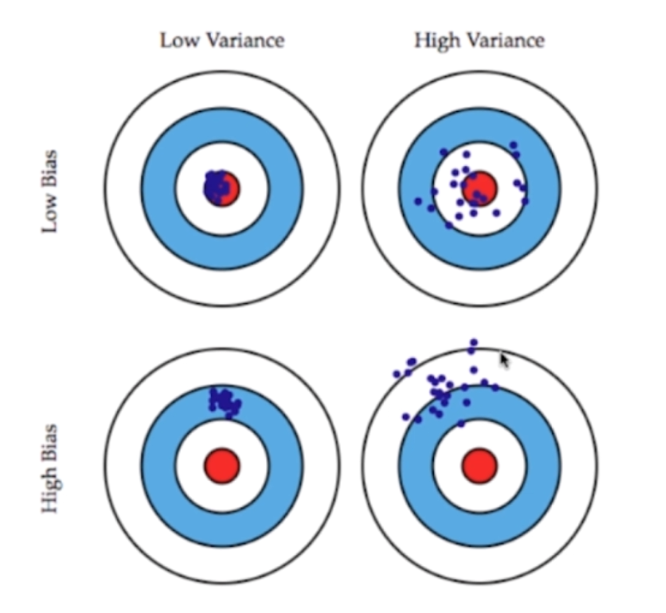
想象我们打靶子,红色的点是中心位置。左上角的图中的蓝色的点均围绕着中心,所以我们说低偏差、低方差;右上角的图也是虽然围绕中心,但是比较分散,所以我们说低偏差、高方差;左下角的图离中心比较远,但是不分散、比较密集,所以是高偏差、低方差;右下角的图,点不仅离得远、还比较分散,所以是高偏差、高方差。
我们训练模型预测数据,就可以看成是打靶,中心的位置是真实的结果。因此我们模型产生的误差,是由三方面所构成。偏差、方差、不可避免的误差
其中不可避免的误差是指,客观存在,由于各种原因使得我们无能为力去改变的误差。比如我们采集过来的数据本身就是含有噪音的,这是我们去不掉的。但是偏差和方差使我们可以通过优化算法去改变的。
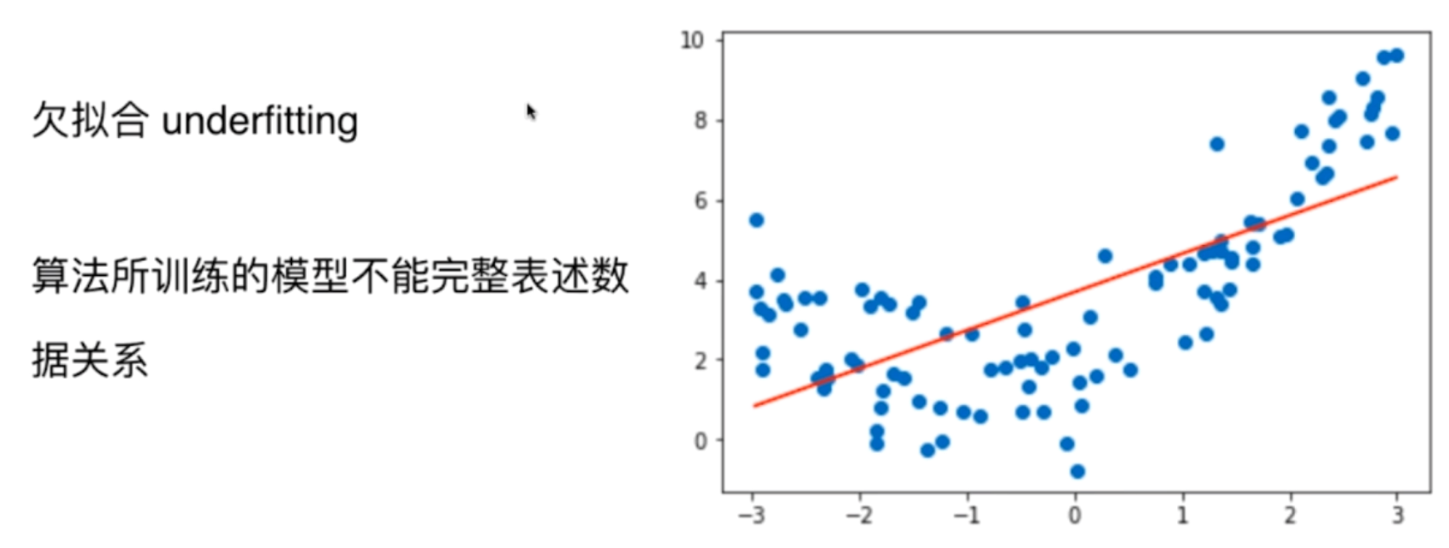
导致偏差的主要原因就是对问题本身的假设不够准确,比如:对非线性数据使用了线性回归法。欠拟合就是个典型,或者我们使用了错误的特征对样本进行了预测等等。
数据的一点点扰动都会较大的影响模型,通常方差较高的原因,是使用的模型太复杂,比如高阶多项式回归。过拟合
有些算法天生是高方差的算法,比如knn。像非参数学习通常都是高方差算法,因为不对数据进行任何的假设。
有些算法天生就是高偏差的算法,比如线性回归。参数学习通常都是高偏差的算法,因为对数据具有极强的假设性。
大多数算法具有相应的参数,可以调整偏差和方差,如KNN中的K,如线性回归中使用多项式回归。
但是偏差和方差通常是矛盾的,降低偏差会提高方差,降低方差会提高偏差。因此我们一般都会在偏差和方差找到一个平衡,而不是集中在一个方向上。
当然在机器学习领域,主要的挑战是来自于方差,而不是偏差,当然这仅局限与算法层面上。比如一些金融数据,用历史的金融数据来预测未来的走向,大多数都不太理想,因为过去的数据不能反映未来的情况,这样使用历史数据容易造成较大的偏差,但是在算法层面上我们不考虑这一点。而就方差来说,我们很容易就让我们的模型非常的复杂,偏差非常的低,而这样的模型具有很高的方差,它的泛化能力很差,最终也没有很好的表现。因此解决过拟合的问题,是很多机器学习算法工程师都要面临的问题的,那么要如何解决呢?
解决高方差的通常手段
1.降低模型复杂度2.减少数据维度;降噪3.增加样本数4.使用验证集5.模型正则化:非常重要的一种方式,后面会介绍。
(八)模型泛化与领回归
之前说过在降低样本方差的时候,有一个重要的手段叫做模型正则化(regularization),那么什么是模型正则化呢?
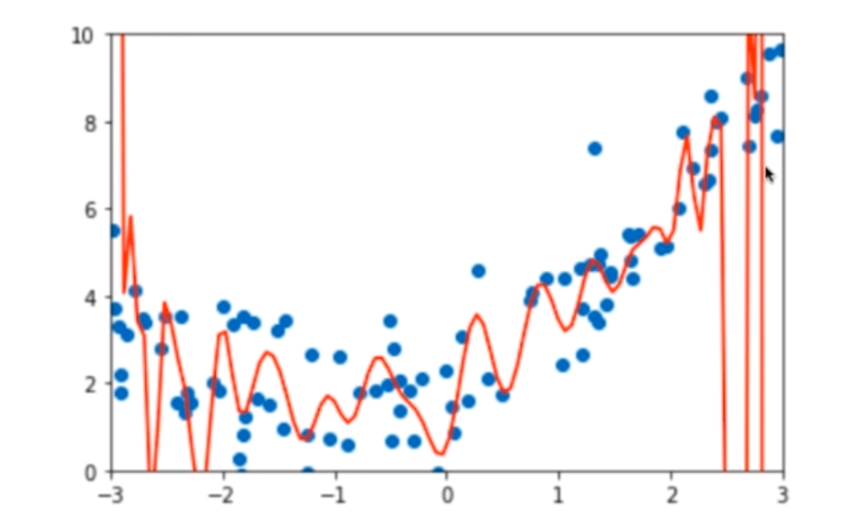
这张图像上的线条比较陡峭,说明某些项的系数非常的大,正则化就是限制某些参数的大小。以线性回归为例:
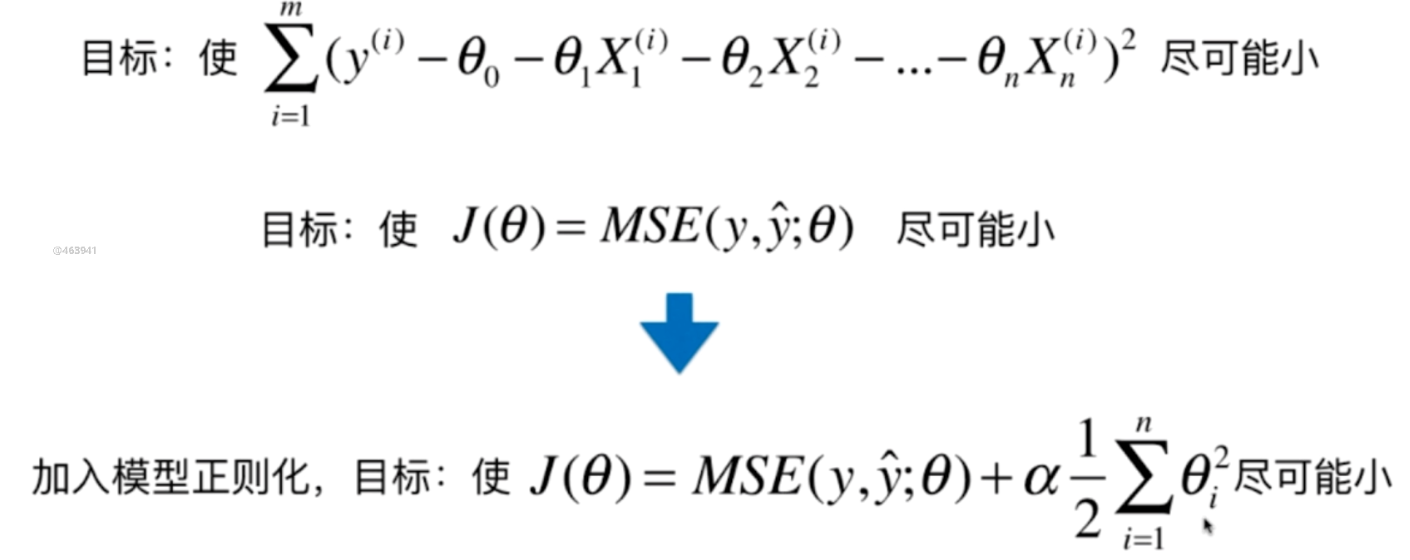
我们原来的目的是找到一个θ,使得MSE(y, ŷ)最小,但是由于θ的某些分量比较大的话,导致MSE较大,那么我们再加上一项,加上θ每一个分量的平方和再乘上一个常数,使得这个结果尽可能的小。
但是注意的是,θ每一分量的平方和,是不包括θ0的,因为θ0表示的截距,它只决定曲线的高低,不决定曲线的陡峭。而且前面乘上了一个二分之一,这个二分之一乘不乘都无所谓,只是在求导的时候能够约掉,方便计算。而α表示正则化所占的比重,而这种模型正则化的方式又被称之为岭回归
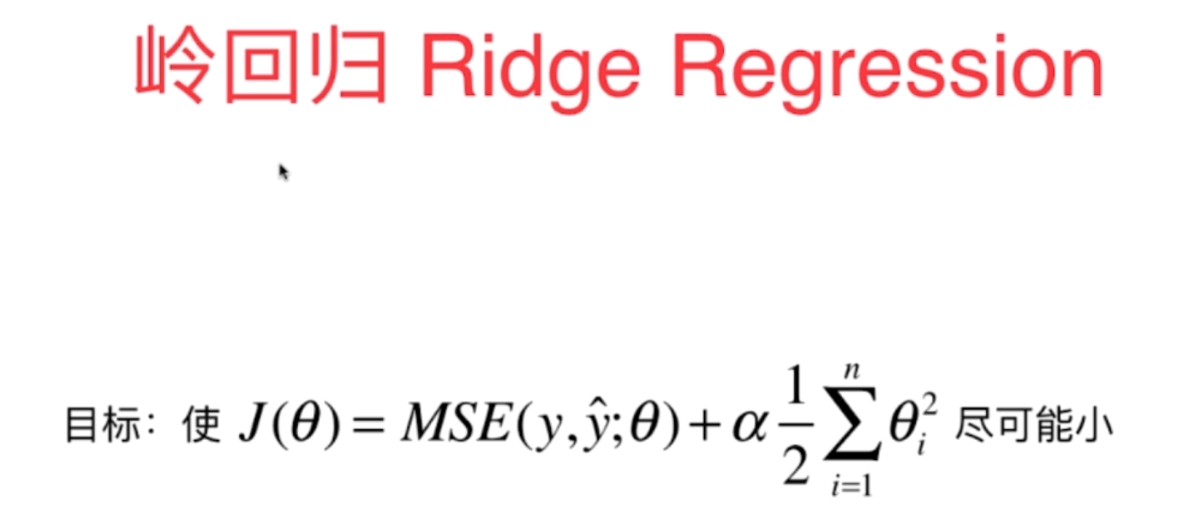
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge, LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler, PolynomialFeatures
from sklearn.pipeline import Pipeline
from sklearn.metrics import mean_squared_error
X = np.random.uniform(-3, 3, size=(100, 1))
y = 0.5 * X + 3 + np.random.normal(0, 1, (100, 1))
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
def RidgeRegression(degree, alpha):
return Pipeline([
("多项式", PolynomialFeatures(degree)),
("数据标准化", StandardScaler()),
# 使用岭回归,里面的alpha参数就是我们图中的α
("岭", Ridge(alpha))
])
def PolyRegression(degree):
return Pipeline([
("多项式", PolynomialFeatures(degree)),
("数据标准化", StandardScaler()),
# 使用岭回归
("线性回归", LinearRegression())
])
ridge = RidgeRegression(20, 0.0001)
poly = PolyRegression(20)
ridge.fit(X_train, y_train)
poly.fit(X_train, y_train)
ridge_y_predict = ridge.predict(X_test)
poly_y_predict = poly.predict(X_test)
print(f"ridge_error:{mean_squared_error(y_test, ridge_y_predict)}") # ridge_error:1.8652125310386714
print(f"poly_error:{mean_squared_error(y_test, poly_y_predict)}") # poly_error:228.94379539427212
"""
可以看到使用岭回归比单纯的使用多项式(线性)回归,效果要好很多
这就是加入模型正则化的威力
"""
所以alpha也是一个超参数,当alpha取值越大,绘制出来的图像也就越平滑,如果取值过大就变成了了一条直线,因此不同的模型,要寻找不同的alpha。
(九)LASSO回归
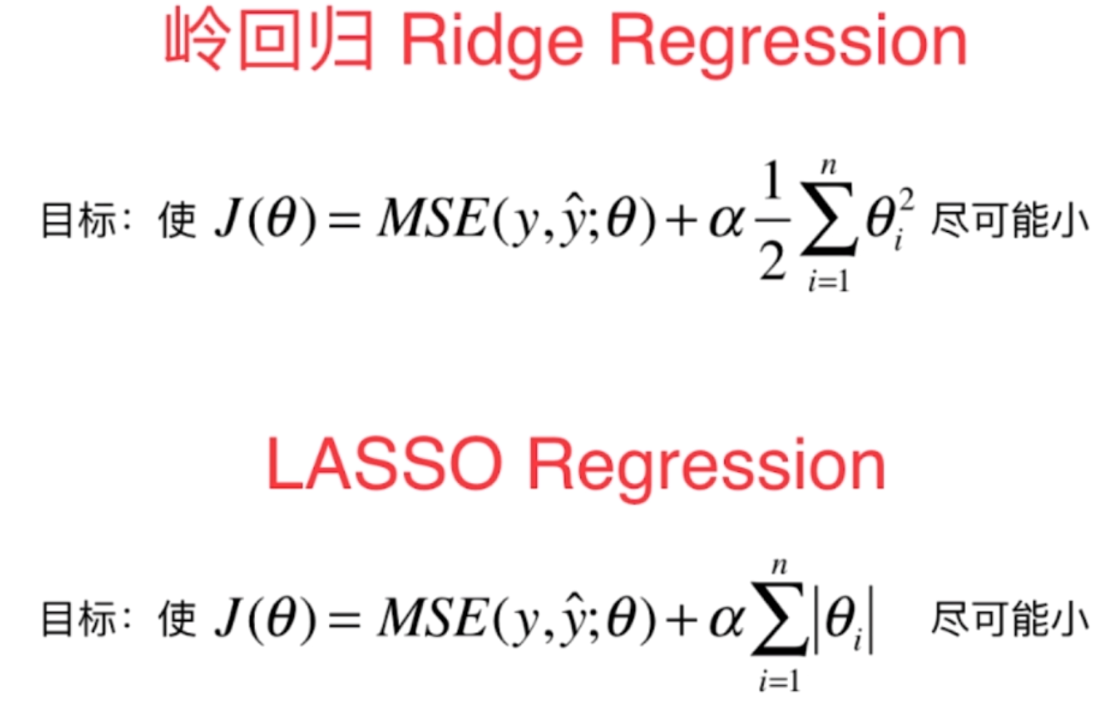
可以看到LASSO回归和岭回归基本一致,只不过在对θ如何表现,或者如何正则化是不一致的。那么具体有什么区别呢?好像在数学意义上是差不多的,那么我们就实际编程实现一下
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge, Lasso
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler, PolynomialFeatures
from sklearn.pipeline import Pipeline
from sklearn.metrics import mean_squared_error
X = np.random.uniform(-3, 3, size=(100, 1))
y = 0.5 * X + 3 + np.random.normal(0, 1, (100, 1))
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
def RidgeRegression(degree, alpha):
return Pipeline([
("多项式", PolynomialFeatures(degree)),
("数据标准化", StandardScaler()),
# 使用岭回归,里面的alpha参数就是我们图中的α
("岭", Ridge(alpha))
])
def LassoRegression(degree, alpha):
return Pipeline([
("多项式", PolynomialFeatures(degree)),
("数据标准化", StandardScaler()),
# 使用岭回归
("线性回归", Lasso(alpha))
])
ridge = RidgeRegression(20, 0.0001)
# 为什么这个传0.01呢?因为在岭回归中,θ带了一个平方
lasso = LassoRegression(20, 0.01)
ridge.fit(X_train, y_train)
lasso.fit(X_train, y_train)
ridge_y_predict = ridge.predict(X_test)
lasso_y_predict = lasso.predict(X_test)
print(f"ridge_error:{mean_squared_error(y_test, ridge_y_predict)}") # ridge_error:1.1861638041634175
print(f"lasso_error:{mean_squared_error(y_test, lasso_y_predict)}") # lasso_error:0.9939705235477055

(十)L1,L2和弹性网络
我们说过岭回归和lasso回归,都是在原来的函数中加上了一项。这一项的作用都是期望能够尽量的减少我们学习到的θ的大小,使得我们得到的模型的泛化能力更强一些。
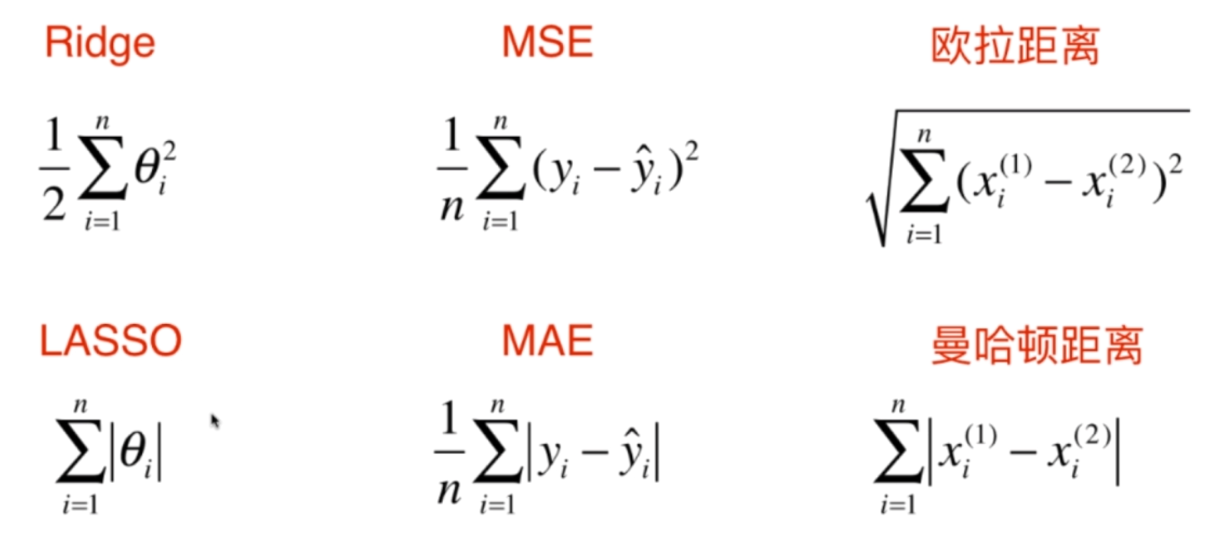
可以看到岭回归和lasso回归进行正则化添加的项类似于MSE和MAE,以及欧拉距离和曼哈顿距离。Ridge和Lasso是衡量正则化的,MSE和MAE是衡量模型的好坏,欧拉距离和曼哈顿距离则是对距离的定义。但是它们背后的本质是类似,只不过应用的场景不一样罢了。
话说还记得闵可夫斯基距离吗?

如果我们再做一下变换的话,只针对一个向量的话,可以写成这样
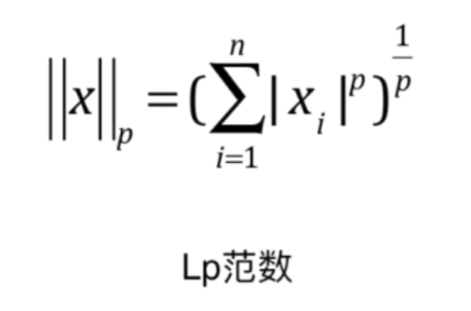
对于任何一个向量,我们将其每一个维度进行p次方求和再开p次方,然后得到的结果我们称之为Lp范数,如果p取1,那么就是L1范数,描述的是零点到x的曼哈顿距离,p取2,那么就是L2范数,描述的是零点到x的欧拉距离。
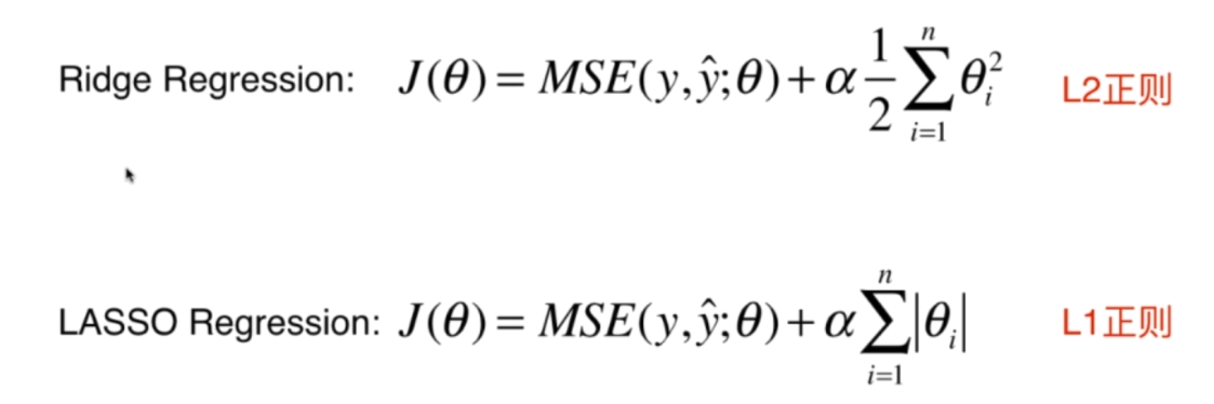
那么可以看到,岭回归实际上给原来的目标函数添加一个L2正则项,LASSO回归实际上是给原来的目标函数添加一个L1正则项。
下面介绍一下弹性网,这又是什么?
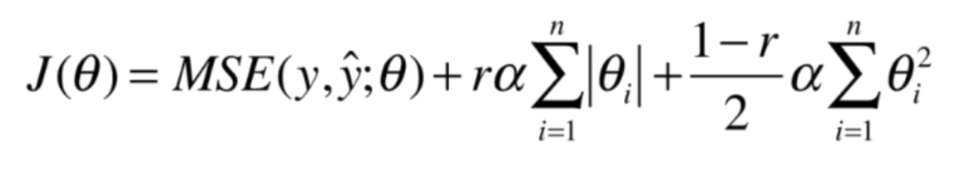
可以看到弹性网是将L1和L2综合起来了,至于前面的r则是L1和L2分别所占的比例。类似于小梯度下降法,也是使用了结合的方式,将批量梯度下降和随机梯度下降结合在了一起。
这一张我们通过多项式回归引出了模型泛化,我们不是为了在训练集上面表现的好,而是希望在应对未来、未知的数据,有比较好的结果,因此我们引入很多方法,如:学习曲线、交叉验证、正则化等等,都是为了让模型泛化能力更强。这就类似于高考,我们平时做的大量的练习题就相当于训练集,之所以进行训练,不是为了在训练集上面表现的有多好,而是增强我们的解题能力(对应模型的泛化能力),来在高考中面对未知的题能有更好的表现。