1 甜在心馒头店
公司楼下有家馒头店:
每天早上六点到十点营业,生意挺好,就是发愁一个事情,应该准备多少个馒头才能既不浪费又能充分供应?
老板统计了一周每日卖出的馒头(为了方便计算和讲解,缩小了数据):
均值为:
按道理讲均值是不错的选择(参见如何理解最小二乘法?),但是如果每天准备5个馒头的话,从统计表来看,至少有两天不够卖, 的时间不够卖:
你“甜在心馒头店”又不是小米,搞什么饥饿营销啊?老板当然也知道这一点,就拿起纸笔来开始思考。
2 老板的思考
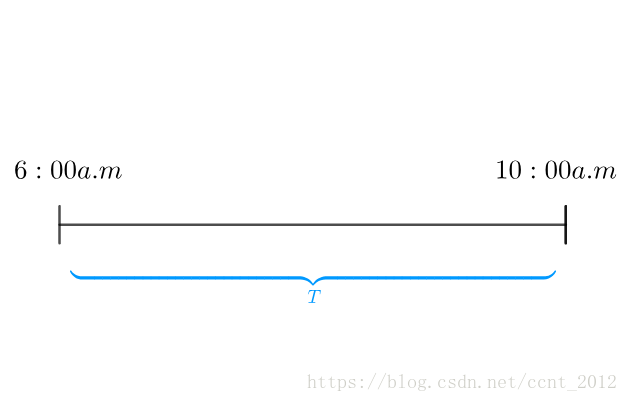
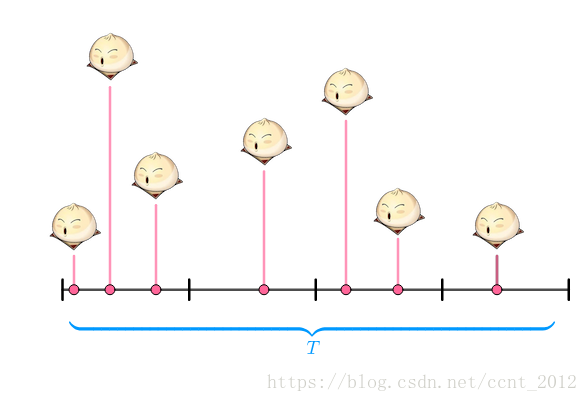
老板尝试把营业时间抽象为一根线段,把这段时间用 来表示:
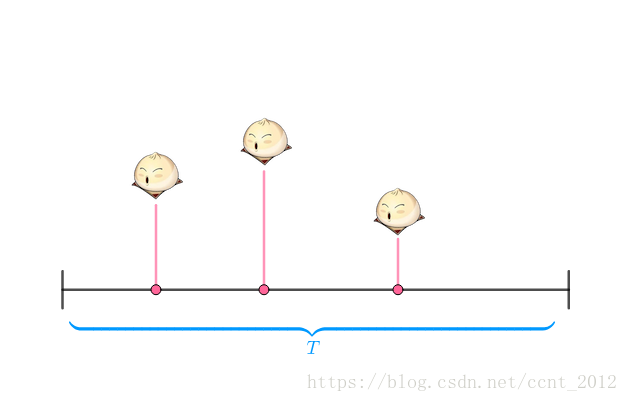
然后把周一的三个馒头(“甜在心馒头”,有褶子的馒头)按照销售时间放在线段上:
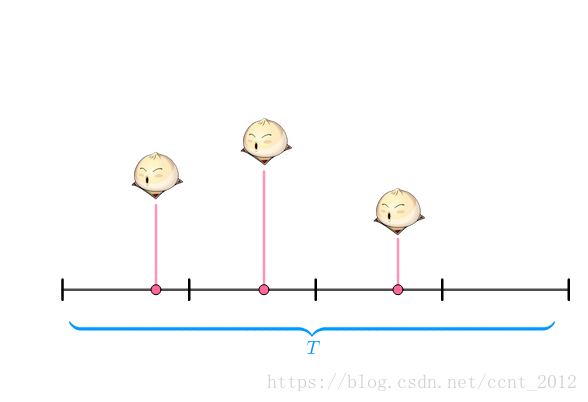
把 均分为四个时间段:
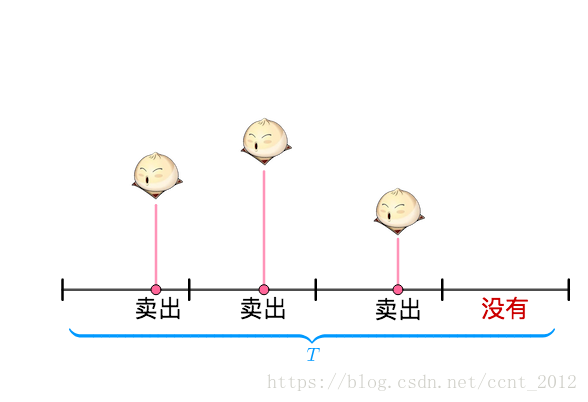
此时,在每一个时间段上,要不卖出了(一个)馒头,要不没有卖出:
在每个时间段,就有点像抛硬币,要不是正面(卖出),要不是反面(没有卖出):
内卖出3个馒头的概率,就和抛了4次硬币(4个时间段),其中3次正面(卖出3个)的概率一样了。
这样的概率通过二项分布来计算就是:
但是,如果把周二的七个馒头放在线段上,分成四段就不够了:
从图中看,每个时间段,有卖出3个的,有卖出2个的,有卖出1个的,就不再是单纯的“卖出、没卖出”了。不能套用二项分布了。
解决这个问题也很简单,把 分为20个时间段,那么每个时间段就又变为了抛硬币:
这样, 内卖出7个馒头的概率就是(相当于抛了20次硬币,出现7次正面):
为了保证在一个时间段内只会发生“卖出、没卖出”,干脆把时间切成 份:
越细越好,用极限来表示:
更抽象一点, 时刻内卖出
个馒头的概率为:
3 的计算
“那么”,老板用笔敲了敲桌子,“只剩下一个问题,概率 怎么求?”
在上面的假设下,问题已经被转为了二项分布。二项分布的期望为:
那么:
4 泊松分布
有了 了之后,就有:
我们来算一下这个极限:
其中:
所以:
上面就是泊松分布的概率密度函数,也就是说,在 时间内卖出
个馒头的概率为:
一般来说,我们会换一个符号,让 ,所以:
这就是教科书中的泊松分布的概率密度函数。
5 馒头店的问题的解决
老板依然蹙眉,不知道 啊?
没关系,刚才不是计算了样本均值:
可以用它来近似:
于是:
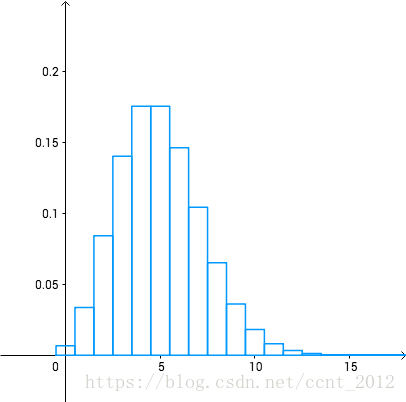
画出概率密度函数的曲线就是:
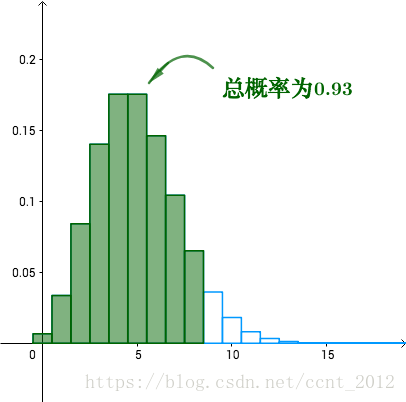
可以看到,如果每天准备8个馒头的话,那么足够卖的概率就是把前8个的概率加起来:
这样 的情况够用,偶尔卖缺货也有助于品牌形象。
老板算出一脑门的汗,“那就这么定了!”
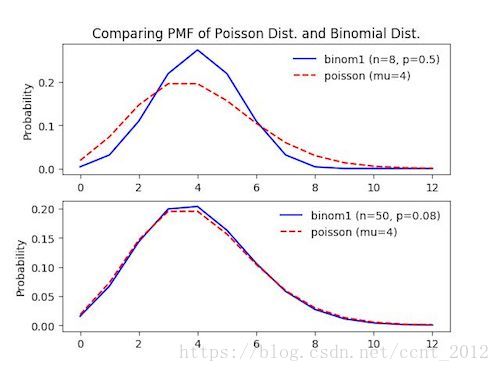
6 二项分布与泊松分布
鉴于二项分布与泊松分布的关系,可以很自然的得到一个推论,当二项分布的 很小的时候,两者比较接近:
7 总结
这个故事告诉我们,要努力学习啊,要不以后馒头都没得卖。
生活中还有很多泊松分布。比如物理中的半衰期,我们只知道物质衰变一半的时间期望是多少,但是因为不确定性原理,我们没有办法知道具体哪个原子会在什么时候衰变?所以可以用泊松分布来计算。
还有比如交通规划等等问题。
顺着这个故事我们还可以讲解:如何理解指数分布?
文章最新版本在(有可能会有后续更新):如何理解泊松分布?