更好的阅读体验
定义:
半平面:
顾名思义,就是平面的一半。一条直线会把平面分成两部分,就是两个半平面。对于半平面,我们可以用直线方程式如:(ax + by >= c) 表示,更常用的是用直线表示。
半平面交:
顾名思义,就是多个半平面求交集。其结果可能是一个凸多边形、无穷平面、直线、线段、点等。
多边形的核:
如果多边形中存在一个区域使得在区域中可以看到多边形中任意位置(反之亦然),则这个区域就是多边形的核。可以用半平面交来求解。
极点:
点 ((x,y)) 与原点的连线与 (x) 轴的夹角,其范围为 [0,360].
为了方便求解我们假设所有的直线的左侧为我们所需要的半平面。
一般来说求解半平面交有两种方法
① 分治法 (O(nlog_2 n))
② 增量法 (O(nlog_2 n))
但是在这里由于分治法常数较大,代码实现较第二种复杂,所以我们着重介绍第二种方法。
算法流程
① 将所有直线极角排序,角度相同的保留下需要的一个
② 用一个双端队列存储当前半平面交,每次通过判断队首与队尾第一个交点是否满足当前直线来更新
③ 先用队尾判定队首交点是否合法,再用队首判断队尾交点是否合法
④ 最后求出来的半平面交是一个凸多边形
极角排序
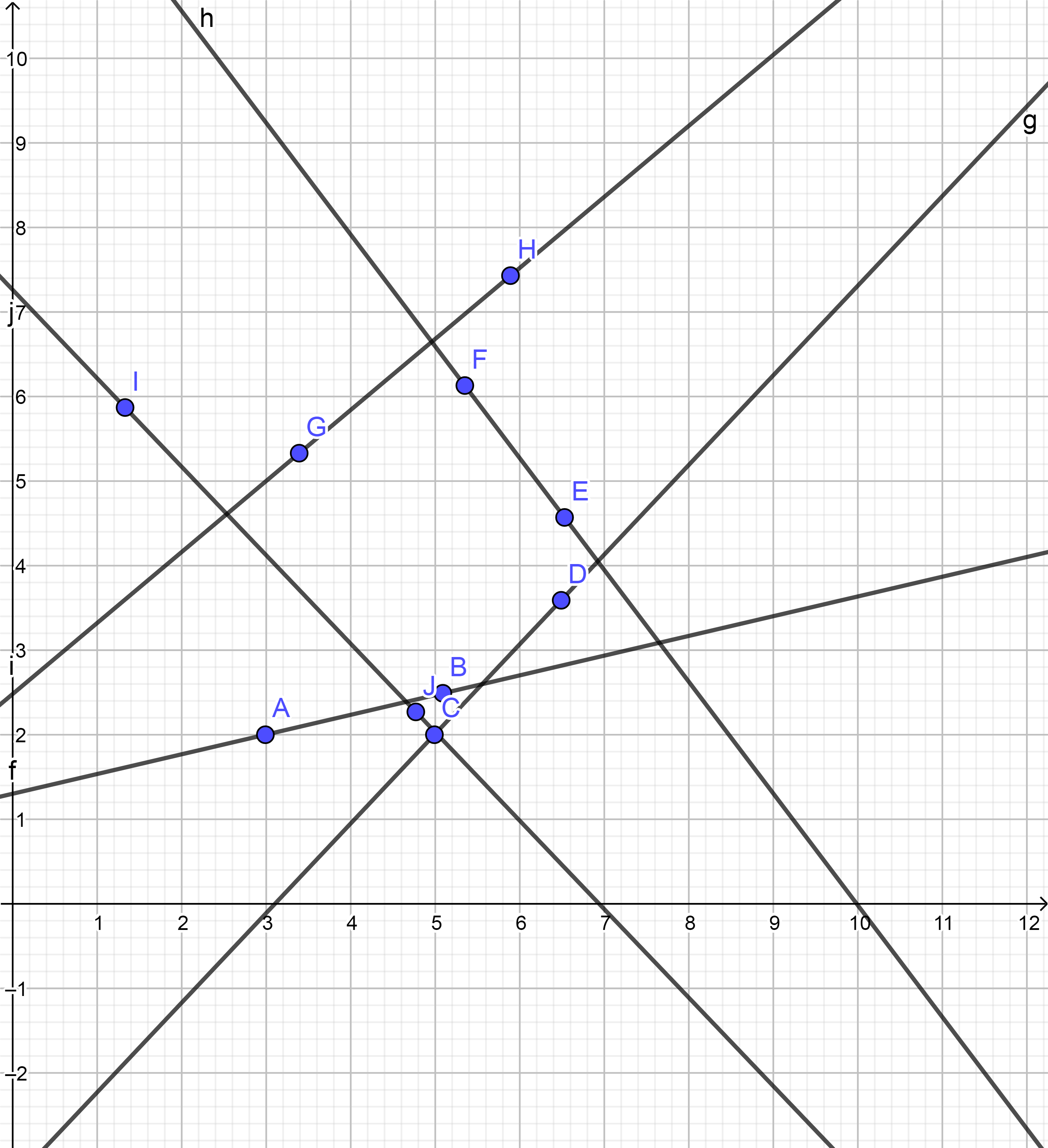
如下图排序后
((a,b),(c,d),(e,f),(g,h),(i,j))
所以我们可以更方便的逆时针依次构造,半平面交
由于我们规定了所有的直线的左侧为我们所需要的半平面
所以极角相同的直线,我们保留最靠左的。
构造半平面交
我们可以依照以下流程来构造一个半平面交,并且构造完成的半平面交有多种情况
① 直线、线段、点不合法
② 凸多边形,无穷平面(可以增加4个用于限制的半平面,使得平面变得有限)
我们维护两个双端队列
一个储存当前有用的直线(半平面),一个储存半平面交的点。
我们依次加入每一条直线(半平面),在加入之前先将之前保存了的点,但不是最终半平面交中的点弹出队列
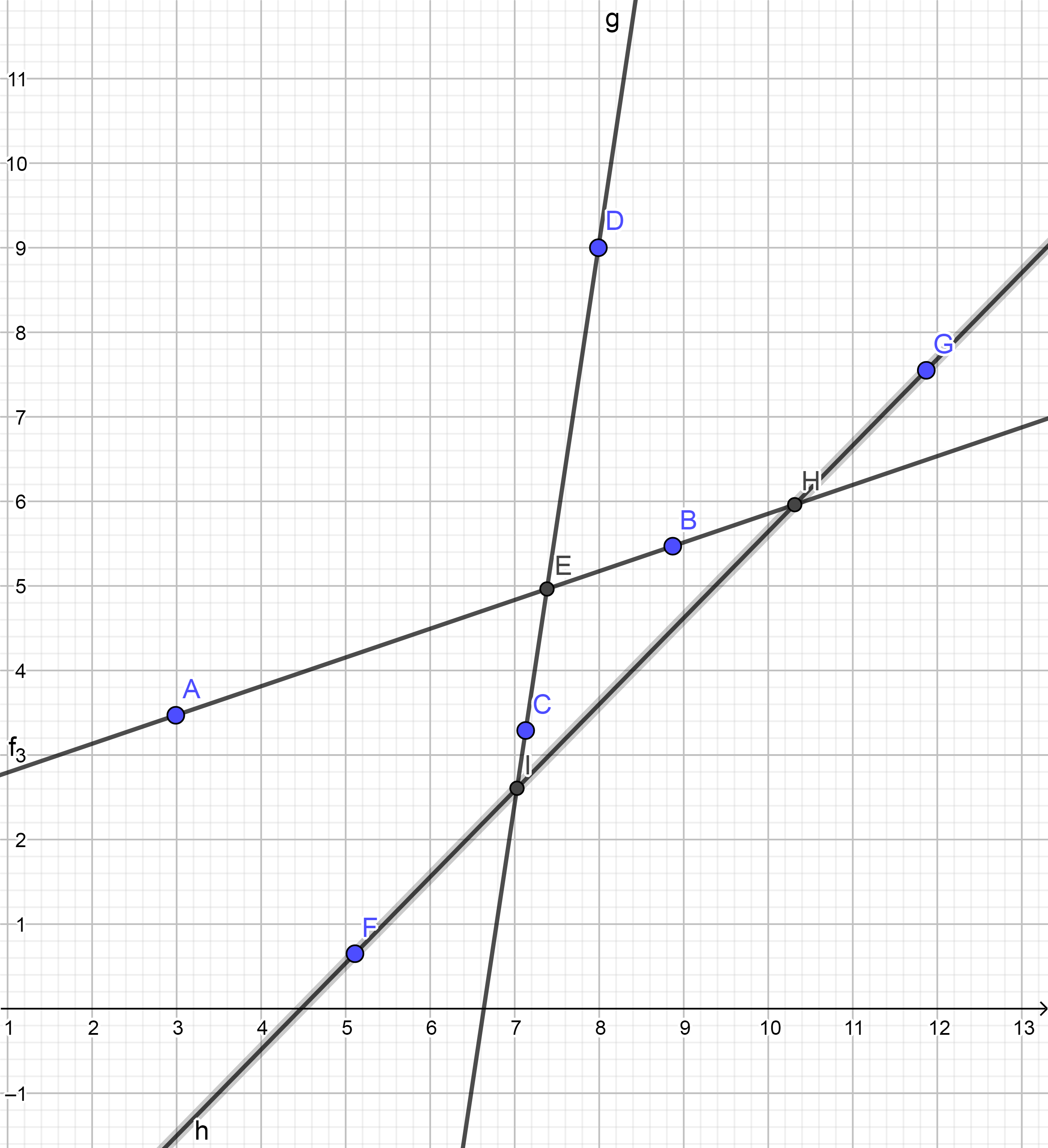
如下图我们首先让 直线(AB) 进入队列,再加入直线(FG),并且求出 (AB) 与 (FG) 的交点 (H),并且把它加入第二个队列里
那么加入 直线(CD) 时我们会发现, (H) 这个点在半平面之外,那么就将它弹出队列,同时将这条边也弹出队列。
所以只要一个点在加入的这条直线的右边我们就将它弹出。
为什么我们要使用双端队列?
可以明显的发现,双端队列的中的点是逆时针排列的
且满足一定的单调性(这个需要自己画图思考,或者配合以下图片思考)
当前加入一条直线,存放点的队列中相邻的两个元素,所对应的直线的极角满足 (angle a<=angle b)((a) 对应点的在队列中的位置位置小于 (b))
那么也就是说,这条直线要么使队首的点处于半平面外,要么使队尾的点处于半平面外
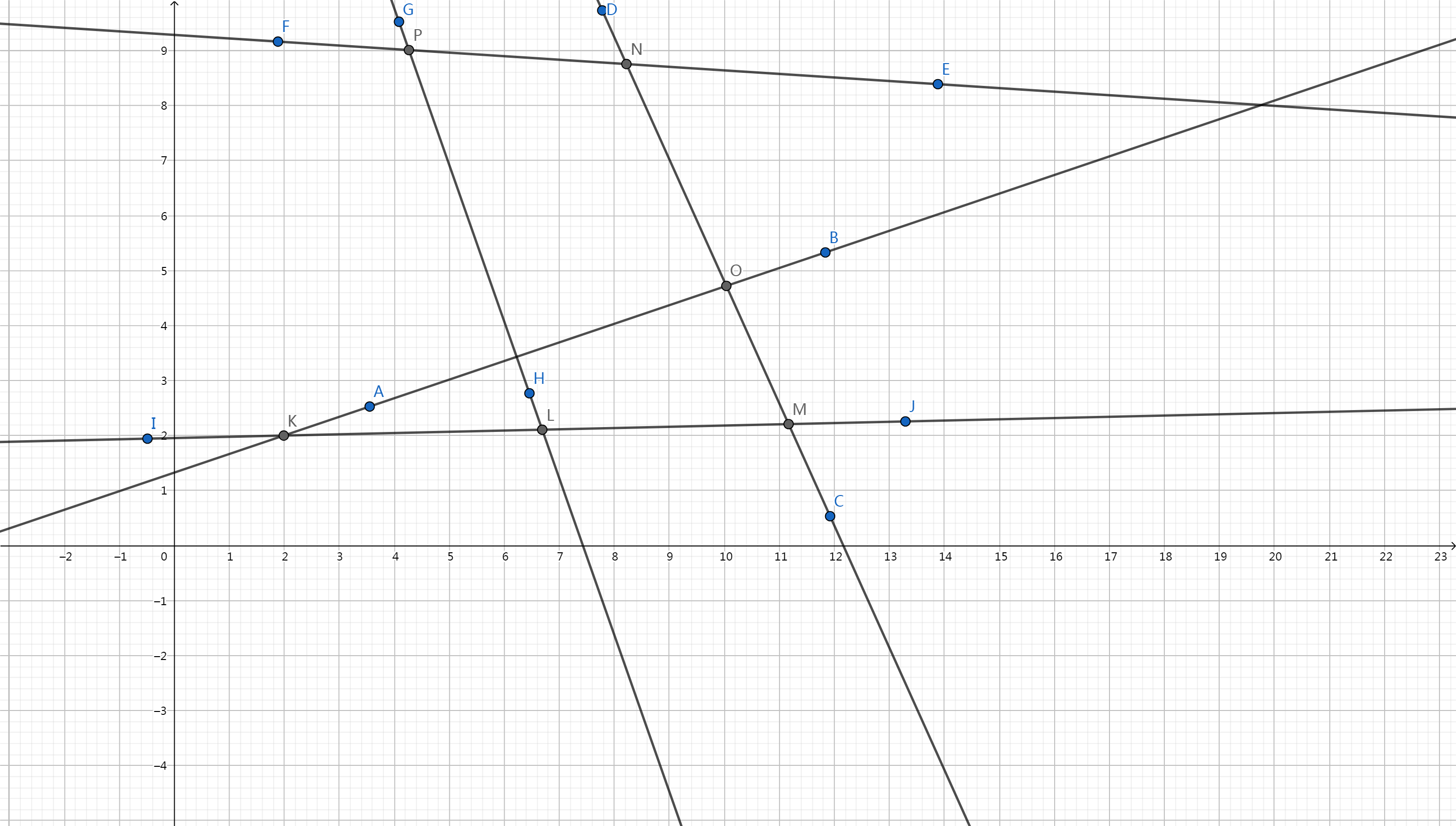
但是因为构造半平面交是环形的构造,如下图
我们顺次处理 (IJ) ,(AB) ,(CD) ,(EF),(GH) 所以当处理到 (GH) 的时候会发现,(K) 点是需要弹出的点但是,(K) 因为在处理 (AB) 时就已经加入了队列而且处在队列的首部,所以我们如果要弹出 (K) 就必须要维护一个双端队列来支持我们的弹出队首的操作。
删去不合法的点
最后队首和队尾都会剩下一些点,它们在半平面交之外
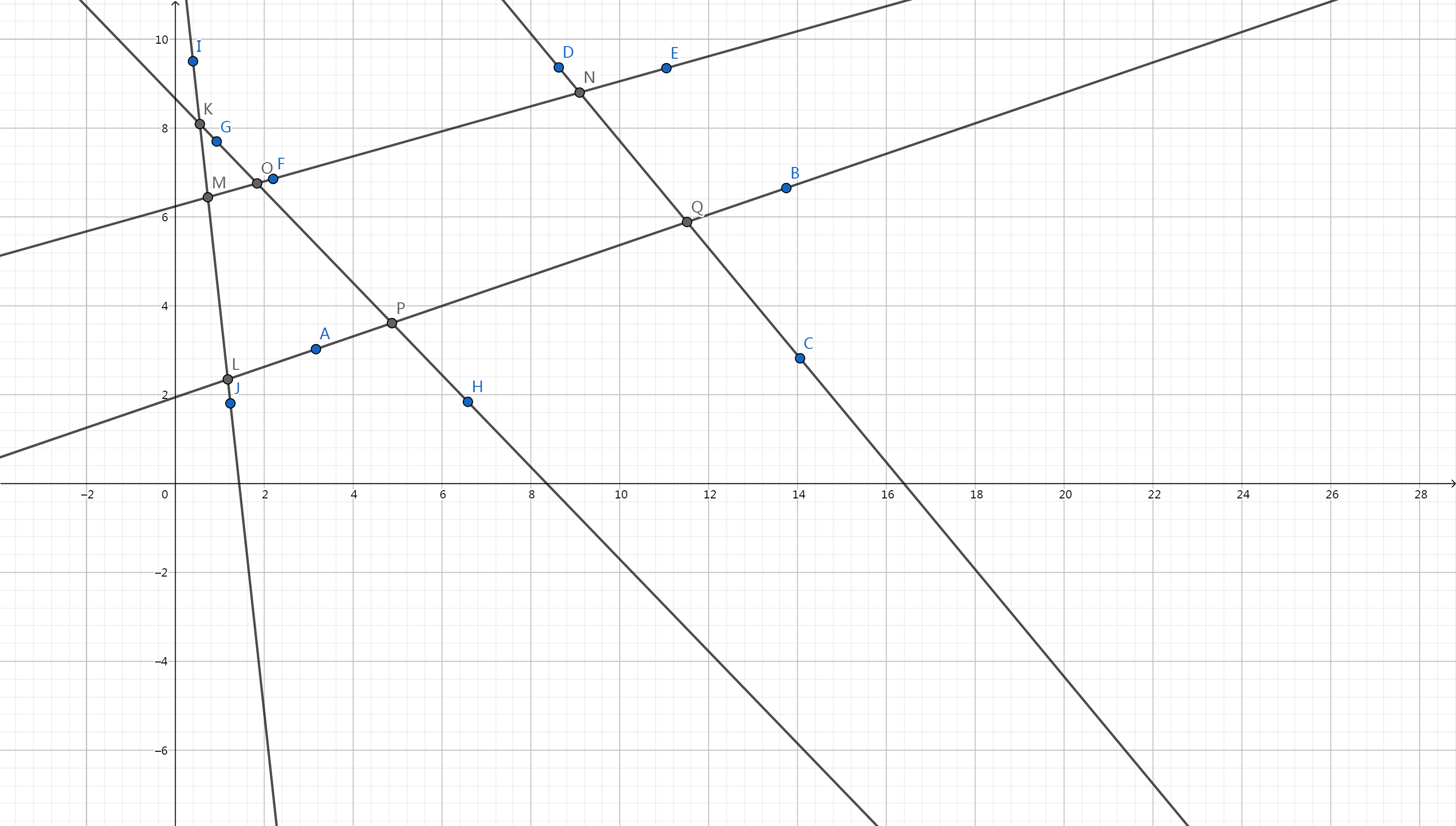
如下图,由于半平面交构造时实际是一个上凸壳和下凸壳,然后是环形的,所以说,会发现某些情况下,有些点多余了
我们需要用队首的直线,判断一下多余的队尾队首的点。
POJ2451模板题,求半平面交面积
AC代码,有注释
#include<cmath>
#include<cstring>
#include<vector>
#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
const double eps=1e-6;
const int maxn=2e5+10;
const double Pi=acos(-1.00);
inline int dcmp(double x)
{
if(x>eps)return 1;
return x<-eps?-1:0;
}
struct Vector
{
double x,y;
Vector(double X=0,double Y=0)
{
x=X,y=Y;
}
bool operator == (const Vector &b)const
{
return dcmp(x-b.x)==0&&dcmp(y-b.y)==0;
}
double angle()
{
return atan2(y,x);//求出极角
}
};
typedef Vector Point;
Vector operator + (Vector a,Vector b){return Vector(a.x+b.x,a.y+b.y);}
Vector operator - (Vector a,Vector b){return Vector(a.x-b.x,a.y-b.y);}
Vector operator * (Vector a,double b){return Vector(a.x*b,a.y*b);}
Vector operator / (Vector a,double b){return Vector(a.x/b,a.y/b);}
struct Line
{
Point s,t;
double ang;
Line(Point X=Vector(),Point Y=Vector())
{
s=X,t=Y,ang=(Y-X).angle();
}
};
typedef Line Segment;
double dot(Vector a,Vector b)
{
return a.x*b.x+a.y*b.y;
}
double cross(Vector a,Vector b)
{
return a.x*b.y-a.y*b.x;
}
bool is_parallel(Line a,Line b)//判断a,b直线是否平行
{
return dcmp(cross(a.t-a.s,b.t-b.s))==0;
}
Point intersection(Line a,Line b)//求出a,b的交点
{
return a.s+(a.t-a.s)*(cross(b.t-b.s,a.s-b.s)/cross(a.t-a.s,b.t-b.s));
}
double area(Point *p,int n)//求出多边形的面积
{
double res=0;
p[n+1]=p[1];
for(int i=1;i<=n;i++)res+=cross(p[i],p[i+1]);
return fabs(res/2);
}
bool operator < (const Line &a,const Line &b)//极角排序,如果极角相同则,选择最靠左的直线
{
double r=a.ang-b.ang;
if(dcmp(r)!=0)return dcmp(r)==-1;
return dcmp(cross(a.t-a.s,b.t-a.s))==-1;
}
bool OnRight(Line a,Point b)//检查b是否在a直线的右边
{
return dcmp(cross(a.t-a.s,b-a.s))<0;
}
bool SI(Line *l,int n,Point *s,int &m)//增量法求半平面交
{
static Line que[maxn];
static Point que2[maxn];//两个双端队列
int head=0,tail=0;
sort(l+1,l+1+n);
que[0]=l[1];
for(int i=2;i<=n;i++)
if(dcmp(l[i].ang-l[i-1].ang)!=0)//极角相等的直线,取一个
{
if(head<tail&&(is_parallel(que[head],que[head+1])||is_parallel(que[tail],que[tail-1])))return false;//如果两个直线共线,但是极角不同,则没有半平面交
while(head<tail&&OnRight(l[i],que2[tail-1]))tail--;//如果在直线右边,删除点
while(head<tail&&OnRight(l[i],que2[head]))head++;
que[++tail]=l[i];
if(head<tail)que2[tail-1]=intersection(que[tail],que[tail-1]);//加入新点
}
while(head<tail&&OnRight(que[head],que2[tail-1]))tail--;//删去多余点
while(head<tail&&OnRight(que[tail],que2[head]))head++;
if(tail-head<=1)return false;//只有一个点或零个点,没有半平面交
que2[tail]=intersection(que[head],que[tail]);//加入最后一条边,和第一条边的交点
m=0;
for(int i=head;i<=tail;i++)s[++m]=que2[i];
return true;
}
const double lim=10000;
int n,m;
Point p[maxn];
Line l[maxn];
double solve()
{
Point a=Point(0,0);//加入最大限制,防止半平面交无限大
Point b=Point(lim,0);
Point c=Point(lim,lim);
Point d=Point(0,lim);
l[++n]=Line(a,b);
l[++n]=Line(b,c);
l[++n]=Line(c,d);
l[++n]=Line(d,a);
if(!SI(l,n,p,m))return 0;
return area(p,m);
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
Point a,b;
scanf("%lf%lf%lf%lf",&a.x,&a.y,&b.x,&b.y);
l[i]=Line(a,b);
}
printf("%.1f
",solve());
}