- 线性回归原理复习
1)构建模型
|_> y = w1x1 + w2x2 + …… + wnxn + b
2)构造损失函数
|_> 均方误差
3)优化损失
|_> 梯度下降
- 实现线性回归的训练
准备真实数据
100样本
x 特征值 形状 (100, 1) 100行1列
y_true 目标值 (100, 1)
y_true = 0.8x + 0.7 假设特征值和目标值直接的线性关系
假定x 和 y 之间的关系 满足
y = kx + b
k ≈ 0.8 b ≈ 0.7
流程分析:
(100, 1) * (1, 1) = (100, 1)
y_predict = x * weights(1, 1) + bias(1, 1)
1)构建模型: 矩阵:matmul
y_predict = tf.matmul(x, weights) + bias
2)构造损失函数: 平均:reduce_mean 平方: square
error = tf.reduce_mean(tf.square(y_predict - y_true))
3)优化损失: 梯度下降的评估器GradientDescentOptimizer
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.01).minimize(error)
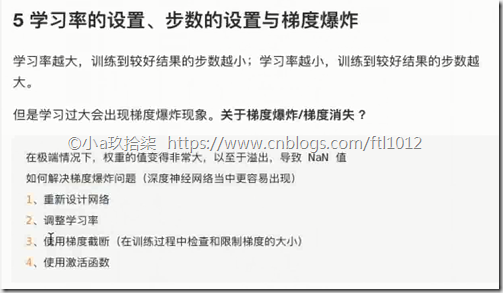
5 学习率的设置、步数的设置与梯度爆炸
- 案例确定
- API
- 步骤分析
demo:
import tensorflow as tf
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
def linear_regression():
"""
自实现一个线性回归
:return:
"""
# 1)准备数据
with tf.variable_scope(name_or_scope='prepare_data'):
X = tf.random_normal(shape=[100, 1], mean=2)
y_true = tf.matmul(X, [[0.8]]) + 0.7 # [[0.8]] 定义了一个一行一列
# 2)构造模型
# 定义模型参数 用 变量
with tf.variable_scope("create_model"):
weights = tf.Variable(initial_value=tf.random_normal(shape=[1, 1])) # 随机产生一个一行一列
bias = tf.Variable(initial_value=tf.random_normal(shape=[1, 1])) # 随机产生一个一行一列
y_predict = tf.matmul(X, weights) + bias
# 3)构造损失函数: 均方误差
with tf.variable_scope("loss_function"):
error = tf.reduce_mean(tf.square(y_predict - y_true))
# 4)优化损失
with tf.variable_scope("optimizer"):
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.01).minimize(error) # 默认0.01
# 显式地初始化变量
init = tf.global_variables_initializer()
with tf.Session() as sess:
# 初始化变量
sess.run(init)
# 查看初始化模型参数之后的值
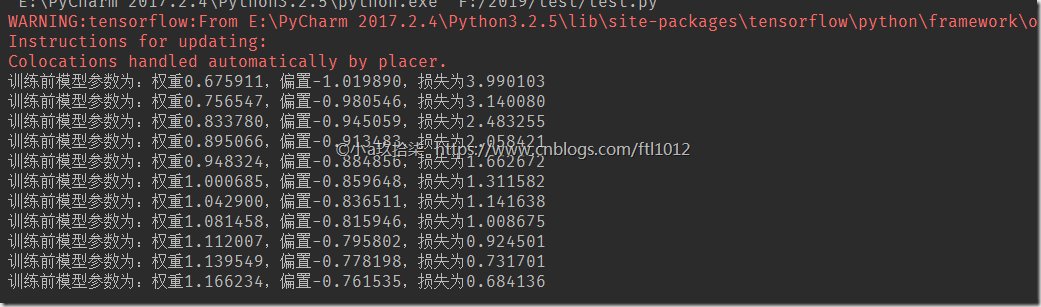
print("训练前模型参数为:权重%f,偏置%f,损失为%f" % (weights.eval(), bias.eval(), error.eval()))
# 开始训练
for i in range(10):
sess.run(optimizer)
print("训练前模型参数为:权重%f,偏置%f,损失为%f" % (weights.eval(), bias.eval(), error.eval()))
if __name__ == "__main__":
linear_regression()
经过上面的训练我们可以发现,在学习率不变的情况下,迭代的次数越多,则效果越好。同理在迭代次数一定的情况下,学习率越高效果越好,但也是有一定限制的。
- 学习率的设置、步数的设置与梯度爆炸
- 变量的trainable设置观察
增加TensorBoard显示
1)创建事件文件
2)收集变量
3)合并变量
4)每次迭代运行一次合并变量
5)每次迭代将summary对象写入事件文件
变量dashboard显示demo:
import tensorflow as tf
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
def linear_regression():
"""
自实现一个线性回归
:return:
"""
# 第一步:
# 1)准备数据
X = tf.random_normal(shape=[100, 1], mean=2)
y_true = tf.matmul(X, [[0.8]]) + 0.7 # [[0.8]] 定义了一个一行一列
# 2)构造模型
# 定义模型参数 用 变量
# trainable=False,的时候则后面的权重会不变,导致损失也不会变化太久,默认True
weights = tf.Variable(initial_value=tf.random_normal(shape=[1, 1]), trainable=True) # 随机产生一个一行一列
bias = tf.Variable(initial_value=tf.random_normal(shape=[1, 1])) # 随机产生一个一行一列
y_predict = tf.matmul(X, weights) + bias
# 3)构造损失函数: 均方误差
error = tf.reduce_mean(tf.square(y_predict - y_true))
# 4)优化损失
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.01).minimize(error)
# 显式地初始化变量
init = tf.global_variables_initializer()
# 第二步:收集变量
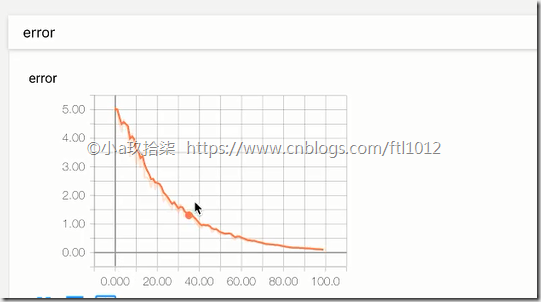
tf.summary.scalar("error", error)
tf.summary.histogram("weights", weights)
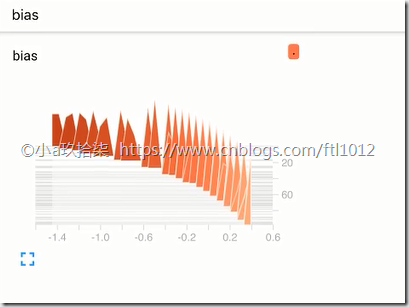
tf.summary.histogram("bias", bias)
# 第三步:合并变量
merged = tf.summary.merge_all()
with tf.Session() as sess:
# 初始化变量
sess.run(init)
# 1_创建事件文件
file_writer = tf.summary.FileWriter("./tmp/", graph=sess.graph)
# 查看初始化模型参数之后的值
print("训练前模型参数为:权重%f,偏置%f,损失为%f" % (weights.eval(), bias.eval(), error.eval()))
# 开始训练
for i in range(100):
sess.run(optimizer)
print("训练前模型参数为:权重%f,偏置%f,损失为%f" % (weights.eval(), bias.eval(), error.eval()))
# 运行合并变量操作
summary = sess.run(merged)
# 将每次迭代后的变量写入事件文件
file_writer.add_summary(summary, i) # i是迭代次数
if __name__ == "__main__":
linear_regression()
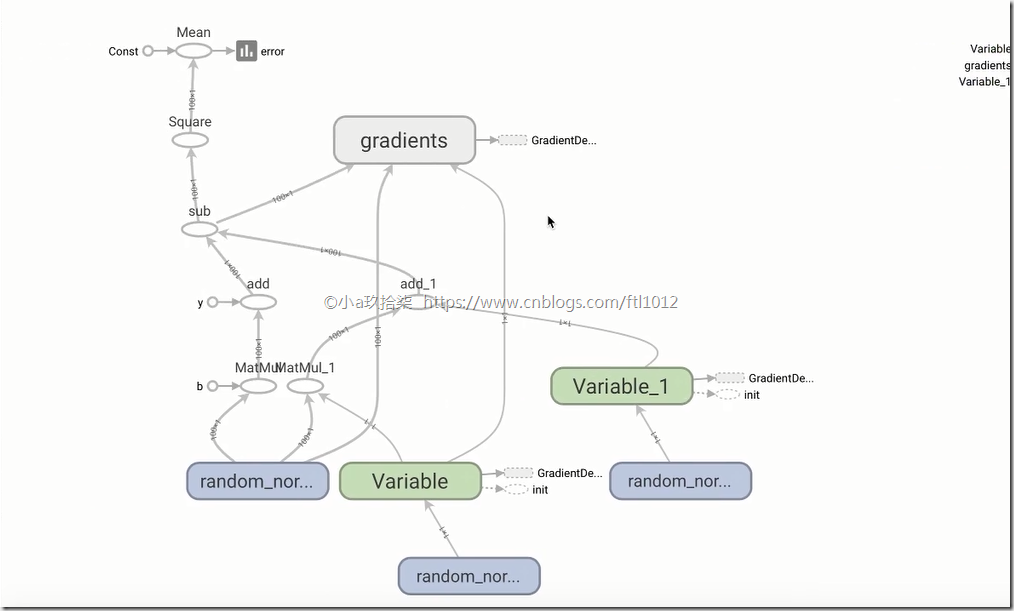
Tensorboard的可视化:http://ftl2018:6006/#graphs&run=.(火狐浏览器)
- 增加命名空间
增加命名空间demo
import tensorflow as tf
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
def linear_regression():
"""
自实现一个线性回归
:return:
"""
# 第一步:
# 1)准备数据
with tf.variable_scope(name_or_scope='prepare_data'):
X = tf.random_normal(shape=[100, 1], mean=2, name='feature')
y_true = tf.matmul(X, [[0.8]]) + 0.7 # [[0.8]] 定义了一个一行一列
# 2)构造模型
# 定义模型参数 用 变量
# trainable=False,的时候则后面的权重会不变,导致损失也不会变化太久,默认True
with tf.variable_scope("create_model"):
weights = tf.Variable(initial_value=tf.random_normal(shape=[1, 1]), trainable=True, name='weights') # 随机产生一个一行一列
bias = tf.Variable(initial_value=tf.random_normal(shape=[1, 1]), name='bias') # 随机产生一个一行一列
y_predict = tf.matmul(X, weights) + bias
# 3)构造损失函数: 均方误差
with tf.variable_scope("loss_function"):
error = tf.reduce_mean(tf.square(y_predict - y_true))
# 4)优化损失
with tf.variable_scope("optimizer"):
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.01).minimize(error)
# 显式地初始化变量
init = tf.global_variables_initializer()
# 第二步:收集变量
tf.summary.scalar("error", error)
tf.summary.histogram("weights", weights)
tf.summary.histogram("bias", bias)
# 第三步:合并变量
merged = tf.summary.merge_all()
with tf.Session() as sess:
# 初始化变量
sess.run(init)
# 1_创建事件文件
file_writer = tf.summary.FileWriter("./tmp/", graph=sess.graph)
# 查看初始化模型参数之后的值
print("训练前模型参数为:权重%f,偏置%f,损失为%f" % (weights.eval(), bias.eval(), error.eval()))
# 开始训练
for i in range(100):
sess.run(optimizer)
print("训练前模型参数为:权重%f,偏置%f,损失为%f" % (weights.eval(), bias.eval(), error.eval()))
# 运行合并变量操作
summary = sess.run(merged)
# 将每次迭代后的变量写入事件文件
file_writer.add_summary(summary, i) # i是迭代次数
if __name__ == "__main__":
linear_regression()

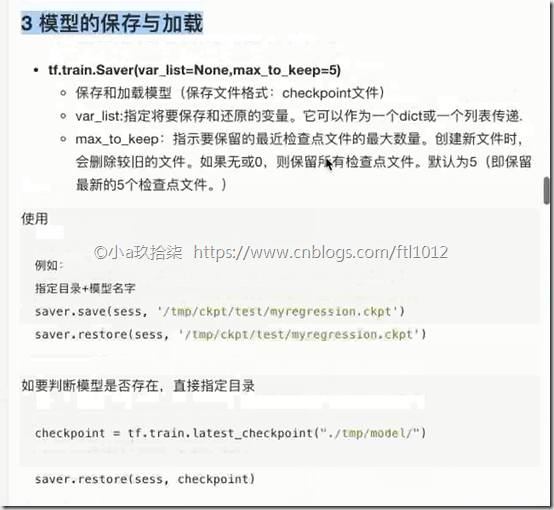
- 模型保存于加载
saver = tf.train.Saver(var_list=None,max_to_keep=5)
1)实例化Saver
2)保存
saver.save(sess, path)
3)加载
saver.restore(sess, path)
模型保存(需要提前准备好目录)与加载demo
import tensorflow as tf
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
def linear_regression():
"""
自实现一个线性回归
:return:
"""
# 第一步:
# 1)准备数据
with tf.variable_scope(name_or_scope='prepare_data'):
X = tf.random_normal(shape=[100, 1], mean=2, name='feature')
y_true = tf.matmul(X, [[0.8]]) + 0.7 # [[0.8]] 定义了一个一行一列
# 2)构造模型
# 定义模型参数 用 变量
# trainable=False,的时候则后面的权重会不变,导致损失也不会变化太久,默认True
with tf.variable_scope("create_model"):
weights = tf.Variable(initial_value=tf.random_normal(shape=[1, 1]), trainable=True, name='weights') # 随机产生一个一行一列
bias = tf.Variable(initial_value=tf.random_normal(shape=[1, 1]), name='bias') # 随机产生一个一行一列
y_predict = tf.matmul(X, weights) + bias
# 3)构造损失函数: 均方误差
with tf.variable_scope("loss_function"):
error = tf.reduce_mean(tf.square(y_predict - y_true))
# 4)优化损失
with tf.variable_scope("optimizer"):
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.01).minimize(error)
# 显式地初始化变量
init = tf.global_variables_initializer()
# 第二步:收集变量
tf.summary.scalar("error", error)
tf.summary.histogram("weights", weights)
tf.summary.histogram("bias", bias)
# 第三步:合并变量
merged = tf.summary.merge_all()
# 保存模型:创建Saver对象
saver = tf.train.Saver(max_to_keep=5)
with tf.Session() as sess:
# 初始化变量
sess.run(init)
# 1_创建事件文件
file_writer = tf.summary.FileWriter("./tmp/", graph=sess.graph)
# 查看初始化模型参数之后的值
print("训练前模型参数为:权重%f,偏置%f,损失为%f" % (weights.eval(), bias.eval(), error.eval()))
# 开始训练
for i in range(100):
sess.run(optimizer)
print("训练前模型参数为:权重%f,偏置%f,损失为%f" % (weights.eval(), bias.eval(), error.eval()))
# 运行合并变量操作
summary = sess.run(merged)
# 将每次迭代后的变量写入事件文件
file_writer.add_summary(summary, i) # i是迭代次数
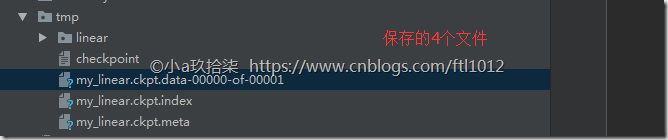
# 保存模型(保存模型参数,而参数在会话中)--》路径需要先创建好
if i % 10 == 0:
saver.save(sess, "./tmp/my_linear.ckpt")
# # 加载模型
# if os.path.exists("./tmp/model/checkpoint"):
# saver.restore(sess, "./tmp/model/my_linear.ckpt")
if __name__ == "__main__":
linear_regression()
- 命令行参数设置
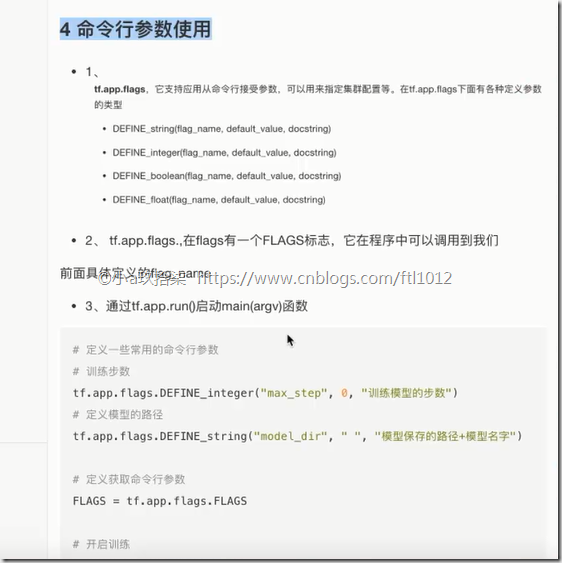
命令行参数使用
1)tf.app.flags
tf.app.flags.DEFINE_integer("max_step", 0, "训练模型的步数")
tf.app.flags.DEFINE_string("model_dir", " ", "模型保存的路径+模型名字")
2)FLAGS = tf.app.flags.FLAGS
通过FLAGS.max_step调用命令行中传过来的参数
3、通过tf.app.run()启动main(argv)函数
具体调用:
命令行demo
import tensorflow as tf
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
# 1)定义命令行参数
tf.app.flags.DEFINE_integer("max_step", 100, "训练模型的步数")
tf.app.flags.DEFINE_string("model_dir", "Unknown", "模型保存的路径+模型名字")
# 2)简化变量名
FLAGS = tf.app.flags.FLAGS
def command_demo():
"""
命令行参数演示
:return:
"""
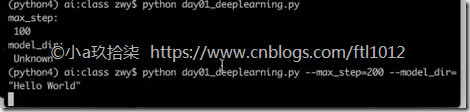
print("max_step:
", FLAGS.max_step)
print("model_dir:
", FLAGS.model_dir)
return None
def main(argv):
print("code start", argv)
return None
if __name__ == "__main__":
# 命令行参数演示
# command_demo()
tf.app.run()