原文链接https://www.cnblogs.com/zhouzhendong/p/Fast-Fourier-Transform.html
多项式 之 快速傅里叶变换(FFT)/数论变换(NTT)/例题与常用套路【入门】 前置技能- 对复数以及复平面有一定的了解
- 对数论要求了解:逆元,原根,中国剩余定理
- 对分治有充足的认识
- 对多项式有一定的认识,并会写 $O(n^2)$ 的高精度乘法
- 多项式定义及基本卷积形式
- $Karatsuba$ 乘法
- 多项式的系数表示与点值表示,以及拉格朗日插值法
- 复数与单位根
- 快速傅里叶变换 $(FFT)$
- 数论变换 $(NTT)$
- 分治 $FFT$
- 拆系数 $FFT$ 和三模数 $NTT$
- 例题与套路
近年来,多项式理论进入中国,在中国 $OI$ 界逐渐占据一方,是一个值得我们去研究的理论。现在, $OI$ 题中出现次数越来越频繁的多项式题,也鼓励了许多 $OIer$ 去学习多项式。
作为多项式的一个重要算法—— $FFT$ ,它有着极其优越的作用。比如,对于初学高精度时的你,是否听说过高精度乘法可以 $O(nlog n)$ ? $FFT$ 可以来解决一类多项式卷积,是生成函数一系列操作的基础,可以解决很多计数问题。
于是,菜鸡博主去学了一下 $FFT$ ,写了这篇总结。
多项式定义及基本卷积形式多项式
定义 多项式 为形如下式的代数表达式。
$$P(x)=sum_{i=0}^{n}a_ix^i=a_0+a_1x+a_2x^2+cdots+a_nx^n$$
其中 $a_0,a_1,a_2,cdots,a_n$ 称为多项式的 系数。
$x$ 没有确定的值。
最高次项的指数 $n$ 叫做多项式的 度 $(Degree,n=deg P)$ ,也可以说是多项式的 次数。
多项式基本卷积形式
下面的这个多项式卷积就是多项式乘法。
定义两个多项式 $g(x),f(x)$ ,设他们的度数分别为 $n,m$ ,则卷积具有如下形式:(设 $g_i$ 为 $g$ 的 $i$ 次项系数, $f_i$ 为 $f$ 的 $i$ 次项系数)
$$h(x)=g(x)f(x)=sum_{i=0}^{n}sum_{j=0}^{m}g_if_jx^{i+j}$$
$$=sum_{i=0}^{n+m}sum_{j=0}^{i}g_jf_{i-j}x^i$$
请务必理解并记住第二行的卷积式,这将会在后面不停的出现。
我们显然可以通过公式来 $O(nm)$ 得到卷积结果。
$Karatsuba$ 乘法针对这种卷积, $Karatsuba$ 提出了下面的这种方法:
对于多项式 $F$ ,我们令 $n=deg F+1$ 。
即多项式可以写成这个形式: $F(x)=sum_{i=0}^{n-1}a_ix^i$ 。
令 $F(x)=F_0(x)+x^{frac n2}F_1(x),G(x)=G_0(x)+x^{frac n2}G_1(x)$ 。
其中, $deg F_0=deg F_1=deg G_0=deg G_1=frac n2$ 。
则
$$(F imes G)(x)=(F_0 imes G_0)(x)+x^{frac n2}(F_0 imes G_1+F_1 imes G_0)(x)+x^n(F_1 imes G_1)(x)$$
令 $M(x)=((F_0+F_1) imes(G_0+G_1))(x)$
我们会开心的发现:
$$(F_0 imes G_1+F_1 imes G_0)(x)=M(x)-(F_0 imes G_0)(x)-(F_1 imes G_1)(x)$$
于是我们只需要计算三个多项式卷积 $M(x),(F_0 imes G_0)(x)-(F_1 imes G_1)(x)$ 即可。
我们采用分治的做法,于是时间复杂度为:
$$T(n)=3T(frac n2)+O(n)=n^{log_23}approx n^{1.585}$$
多项式的系数表示与点值表示,以及拉格朗日插值法系数表示
(令 $n=deg F$ )
这里拿出了最开始提到的多项式:
$$f(x)=a_0+a_1x+a_2x^2+cdots+a_nx^n$$
把 $a$ 数组看作 $n+1$ 维向量 $vec{a}=(a_0,a_1,cdots,a_n)$ ,其 系数表示 就是向量 $vec{a}$ 。
点值表示
(令 $n=deg F$ )
取任意 $n+1$ 个不同的 $x_0,x_1,cdots,x_n$ 代入多项式进行求值,得到了 $n+1$ 个不同的二元组 $(x_0,F(x_0)),(x_1,F(x_1)),cdots,(x_n,F(x_n))$ 。
我们称这 $n+1$ 个点表示多项式的方法叫做多项式的 点值表示 。
这里要注意,多项式的点值表示有无数种,但是多项式的系数表示是唯一的。
拉格朗日插值法
实现系数表示到点值表示的变换,我们可以直接把 $x$ 代入求解,复杂度 $O(n^2)$ 。
但是点值表示转系数表示就没这么简单了。
这里首先提一点:虽然同一个多项式的点值表示有无数种,但是这些点值表示都能唯一的确定一个多项式,唯一的确定一个系数表示。
从点值表示转到系数表示,我们可以使用插值法。
其中拉格朗日插值法能够在 $O(n^2)$ 的复杂度内得到系数表示。
具体在这里不展开介绍了,可以参见:
https://www.zhihu.com/question/58333118/answer/262507694
复数与单位根复数的定义
复数 $(Complex)$ 由实部和虚部组成。
可以写成如下形式:
$$A=a+ib,(a,bin mathbb R,Ainmathbb C)$$
其中 $A$ 就是一个复数。
其中 $i=sqrt{-1}$ ,为虚数单位。
在后面的公式中要注意区分虚数单位 $i$ 和求和指标 ($sum$) $i$ 。
显然这里可以列举三个 $FFT$ 常用的复数运算:
$(A_1,A_2inmathbb C,a_1,b_1,a_2,b_2inmathbb R)$
$$A_1+A_2=(a_1+ib_1)+(a_2+ib_2)=(a_1+a_2)+i(b_1+b_2)$$
$$A_1-A_2=(a_1+ib_1)-(a_2+ib_2)=(a_1-a_2)+i(b_1-b_2)$$
$$A_1 imes A_2=(a_1+ib_1)(a_2+ib_2)=a_1a_2+i^2b_1b_2+ia_1b_2+ia_2b_1\=(a_1a_2-b_1b_2)+i(a_1b_2+a_2b_1)$$
复平面
复平面是个二维平面,其中横轴代表实数,称为实轴。纵轴代表虚数,称为虚轴。
定义复平面上从原点出发的向量$vec{a}=(a,b)$表示虚数$a+ib$。
例如:
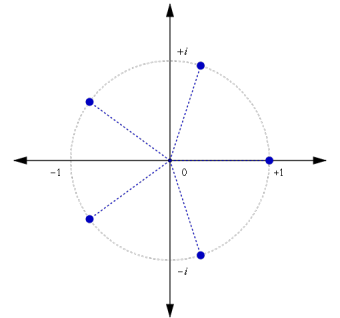
其中的 $5$ 条蓝色向量就代表了 $5$ 个虚数。
关于复数乘法,有一个口诀:模长相乘,幅角相加。
模长就是复数在复平面上表示的向量的模长,幅角就是以正实轴为始边,这个向量为终边所构成的角。
单位根
$n$ 次单位根 $omega_ninmathbb C$ ,满足 $omega_n^n=1$ 。
显然 $n$ 次方程有 $n$ 个解,把他们写在复平面上面,可以把单位圆等分成 $n$ 份。由于复数乘法模长相乘,所以模长永远是 $1$ ,说明他们总在单位圆上。由于幅角相加,得到他们等分单位圆。
于是我们可以写出单位根的表达式:
记 $omega_n=cos(frac{2pi}{n})+isin(frac{2pi}{n})$ ,则 $n$ 次单位根就是 $omega_n^0, omega_n^1, cdots, omega_n^{n-1}$ 。
通项公式, $omega_n^i=cos(frac{2ipi}{n})+isin(frac{2ipi}{n}) (0leq i<n)$
当然,在数学上,单位根还有这种定义: $omega_n=e^{frac{2pi i}{n}}$ ,读者可以尝试通过这个来推导前几个式子,这里不展开介绍。
单位根有一些优秀的性质。
定理1:相消定理
对于任意整数 $ngeq 0,kgeq 0,dgeq 0$ ,有:
$$omega_{dn}^{dk}=e^{frac{2pi dki}{dn}}=e^{frac{2pi ki}{n}}=omega_n^k$$
即:
$$omega_{dn}^{dk}=omega_{n}^{k}$$
定理2:折半定理
对于任意的偶数 $ngeq 0,kgeq 0$ ,有
$$omega_{n}^{k}=omega_{frac n2}^{frac k2}$$
这个由定理1显然可得。
此外,我们还可以从复平面图像的角度理解单位根。

观察任何一个单位根 $omega_{n}^{i}$ ,
$$omega_{n}^{i+1}=omega_{n}^{i} imesomega_{n}^{1}$$
观察其图像,会发现 $ imesomega_{n}^{1}$ 的效果就是把原复数在复平面上的向量绕原点逆时针旋转$frac{2pi}{n}$的角度。
类似的, $ imesomega_{n}^{1}$ 的效果相反,为顺时针方向。
再有,显然, $omega_{n}^{-i}=omega_{n}^{n-i}$ 。
于是对于整数 $i$ ,如果从 $omega_{n}^{0}$ 逆时针旋转一定角度得到的向量为单位根 $omega_{n}^{i}$ ,那么顺时针旋转相同的角度也必然会得到 $omega_{n}^{-i}=omega_{n}^{n-i}$ 。
于是如果把所有 $n$ 次单位根在复平面上画出来,他们是上下对称的。
性质3
所以如果令 $omega_{n}^{k}=a+ib$ ,则 $omega_{n}^{-k}=a-ib (a,bin mathbb R,sqrt{a^2+b^2}=1)$ ,即 $omega_n^{-k}=conj(omega_n^k)$ 。
考虑到 $omega_{n}^{n}$ 是绕着原点转了一圈,那么 $omega_{n}^{frac n2}$ 就是转了半圈,所以 $omega_{n}^{frac n2}=-1$ 。
所以 $omega_{n}^{i}$ 与 $omega_{n}^{i+frac n2}$ 在单位圆上的位置是相对的,因为转了半圈。换句话说:
性质4
$$omega_{n}^{i+frac n2}=omega_{n}^{frac n2}cdotomega_{n}^{i}=-omega_{n}^{i}$$
快速傅里叶变换(Fast Fourier Transform, FFT)回忆一下之前的多项式卷积:
$$h(x)=sum_{i=0}^{n+m}sum_{j=0}^{i}g_jf_{j-i}x^i$$
我们要快速求 $h(x)$ 的每一项系数。
系数表示并不能支持快速的卷积。
但是在点值表示下,却可以在 $O(n)$ 复杂度内快速卷积。
目前的瓶颈在于系数表示与点值表示的快速的相互转化。
由于点值表示有很多种,只要你选择的 $x$ 互不相同即可。于是我们可以考虑选择一些特殊的 $x$ 。
注意,后面为了方便,设多项式的度为 $n-1,(n=2^a,ainmathbb Z)$ ,如果次数不足则高位补上系数 $0$ ,保证任何运算过程中多项式的真的度都小于 $n$ 。
离散傅里叶变换
设有多项式
$$F(x)=sum_{i=0}^{n-1}a_ix^i$$
将 $n$ 个不同的 $n$ 次单位根 $omega_{n}^{0},omega_{n}^{1},cdots,omega_{n}^{n-1}$ 代入到 $F(x)$ 中,得到点值表达式:
$$vec{y}=(F(omega_{n}^{0}),F(omega_{n}^{1}),cdots,F(omega_{n}^{n-1}))$$
于是点值向量 $vec{y}$ 就叫做系数向量 $vec{a}=(a_0,a_1,cdots,a_{n-1})$ 的离散傅里叶变换 $(Discrete Fourier Transform, DFT)$ 。
但是直接代入求值是 $O(n^2)$ 的,我们需要一个更快的求值方法。
令 $F_0(x)=sum_{i=0}^{frac n2-1}a_{2i}x^i,F_1(x)=sum_{i=0}^{frac n2-1}a_{2i+1}x^i$
则:(下面的推导会用到之前介绍过的单位根性质的第2条和第4条)
$$F(x)=F_0(x^2)+xF_1(x^2)$$
$$F(omega_{n}^{i})=F_0(omega_{n}^{2i})+omega_{n}^{i}F_1(omega_{n}^{2i})=F_0(omega_{frac n2}^{i})+omega_{n}^{i}F_1(omega_{frac n2}^{i})$$
$$F(omega_{n}^{i+frac n2})=F(-omega_{n}^{i})=F_0(omega_{n}^{2i})-omega_{n}^{i}F_1(omega_{n}^{2i})=F_0(omega_{frac n2}^{i})-omega_{n}^{i}F_1(omega_{frac n2}^{i})$$
注意: $deg F_0=deg F_1=frac n2$ 。
于是我们可以继续分治,对于 $F_0$ 和 $F_1$ 再继续同样的操作。
时间复杂度:
$$T(n)=2T(frac n2)+O(n)=O(nlog n)$$
逆离散傅里叶变换
现在你需要快速的把点值表达式转换成系数表达式。
与刚才的离散傅里叶变换相反,系数向量 $vec{a}=(a_0,a_1,cdots,a_{n-1})$ 就叫做点值向量 $vec{y}$ 的逆离散傅里叶变换 $(Inverse Discrete Fourier Transform, IDFT)$
首先,我们把刚才的 $DFT$ 过程用矩阵来表示:
$$egin{equation}egin{bmatrix} (omega_n^0)^0 & (omega_n^0)^1 & cdots & (omega_n^0)^{n-1} \ (omega_n^1)^0 & (omega_n^1)^1 & cdots & (omega_n^1)^{n-1} \ vdots & vdots & ddots & vdots \ (omega_n^{n-1})^0 & (omega_n^{n-1})^1 & cdots & (omega_n^{n-1})^{n-1} end{bmatrix} egin{bmatrix} a_0 \ a_1 \ vdots \ a_{n-1} end{bmatrix} = egin{bmatrix} A(omega_n^0) \ A(omega_n^1) \ vdots \ A(omega_n^{n-1}) end{bmatrix}end{equation}$$
我们记左侧的系数矩阵为 $mathbf V$ ,构造矩阵 $d_{i,j}=(omega_{n}^{-i})^j$
$$mathbf D = egin{bmatrix} (omega_n^{-0})^0 & (omega_n^{-0})^1 & cdots & (omega_n^{-0})^{n-1} \ (omega_n^{-1})^0 & (omega_n^{-1})^1 & cdots & (omega_n^{-1})^{n-1} \ vdots & vdots & ddots & vdots \ (omega_n^{-(n-1)})^0 & (omega_n^{-(n-1)})^1 & cdots & (omega_n^{-(n-1)})^{n-1} end{bmatrix}$$
设 $mathbf E=mathbf Dcdotmathbf V$ ,则:
$$egin{eqnarray*} e_{ij} &=& sum_{k=0}^{n-1} d_{ik} v_{kj} \ &=& sum_{k=0}^{n-1} omega_n^{-ik}omega_n^{kj} \ &=& sum_{k=0}^{n-1} omega_n^{k(j-i)}\&=&large{egin{cases}n& ext{$(i=j)$}\ sum_{k=0}^{n-1}(omega_{n}^{j-i})^k=frac{1-(omega_{n}^{j-i})^n}{1-omega_{n}^{j-i}}=0& ext{$(i eq j)$}end{cases}}end{eqnarray*}$$
于是我们发现了一个非常特殊的性质:
$mathbf E$ 是单位矩阵的 $n$ 倍。
也就是 $frac 1nmathbf D=mathbf V^{-1}$ 。
于是我们将 $frac 1nmathbf D$ 在 $(1)$ 式两侧左乘,得到:
$$egin{equation*} egin{bmatrix} a_0 \ a_1 \ vdots \ a_{n-1} end{bmatrix} = frac{1}{n} egin{bmatrix} (omega_n^{-0})^0 & (omega_n^{-0})^1 & cdots & (omega_n^{-0})^{n-1} \ (omega_n^{-1})^0 & (omega_n^{-1})^1 & cdots & (omega_n^{-1})^{n-1} \ vdots & vdots & ddots & vdots \ (omega_n^{-(n-1)})^0 & (omega_n^{-(n-1)})^1 & cdots & (omega_n^{-(n-1)})^{n-1} end{bmatrix} egin{bmatrix} A(omega_n^0) \ A(omega_n^1) \ vdots \ A(omega_n^{n-1}) end{bmatrix} end{equation*}$$
于是只需要把 $omega_{n}^{i}$ 换成 $omega_{n}^{-i}$ (根据单位根性质4,只需要把 $omega_{n}^{i}$ 的虚部取其相反数即可),然后 $DFT$ ,然后将所得的结果除以 $n$ ,就可以实现 $IDFT$ 了。
递归版FFT代码
有同学认为需要加一份递归版的代码。可惜是博主没有写过递归版的。于是就从网上拉了一份QAQ。
void fft(int n, complex<double>* buffer, int offset, int step, complex<double>* epsilon)
{
if(n == 1) return;
int m = n >> 1;
fft(m, buffer, offset, step << 1, epsilon);
fft(m, buffer, offset + step, step << 1, epsilon);
for(int k = 0; k != m; ++k)
{
int pos = 2 * step * k;
temp[k] = buffer[pos + offset] + epsilon[k * step] * buffer[pos + offset + step];
temp[k + m] = buffer[pos + offset] - epsilon[k * step] * buffer[pos + offset + step];
}
for(int i = 0; i != n; ++i)
buffer[i * step + offset] = temp[i];
}
//http://blog.miskcoo.com/2015/04/polynomial-multiplication-and-fast-fourier-transform#IDFT迭代版FFT与蝴蝶操作
你显然已经可以递归实现 $FFT$ 了。但是递归实现 $FFT$ 常数较大,代码又长,一般不写。
假设现在有 $8$ 个数要进行 $DFT$ ,我们来看看递归的时候,每一个数的顺序以及二进制位的情况。
$$egin{vmatrix}000&&001&&010&&011&&100&&101&&110&&111\0&&1&&2&&3&&4&&5&&6&&7\0&&2&&4&&6&|&1&&3&&5&&7\0&&4&|&2&&6&|&1&&5&|&3&&7\0&|&4&|&2&|&6&|&1&|&5&|&3&|&7\000&&100&&010&&110&&001&&101&&011&&111end{vmatrix}$$
稍微观察一下,你就会发现,分治到边界之后的下标是原下标的二进制位翻转。
于是我们只需要预处理每一个数的二进制位翻转后的结果,并在 $FFT$ 开始前交换所有数与他翻转之后的数。具体可以参见后面的代码。
蝴蝶操作
在合并两个子问题的过程中,假设 $A_0(omega_{frac n2}^{k})$ 和 $A_1(omega_{frac n2}^{k})$ 分别保存在 $a_k$ 和 $a_{frac n2+k}$ 中,而 $A(omega_{n}^{k})$ 和 $A(omega_{n}^{k+frac n2})$ 将会被放在之后的 $a_k$ 和 $a_{frac n2+k}$ 中,为了避免覆盖原值出错,我们加入一个临时变量,并实现以下三个操作:
$$tmpleftarrow omega_{n}^{k} imes a_{frac n2+k}$$
$$a_{frac n2+k}leftarrow a_k-tmp$$
$$a_kleftarrow a_k + tmp$$
这个操作被叫做蝴蝶操作。
迭代版FFT模版 -UOJ#34多项式乘法
#include <bits/stdc++.h>
using namespace std;
const int N=1<<20;
const double PI=acos(-1.0);
struct C{
double r,i;
C(){}
C(double a,double b){r=a,i=b;}
C operator + (C x){return C(r+x.r,i+x.i);}
C operator - (C x){return C(r-x.r,i-x.i);}
C operator * (C x){return C(r*x.r-i*x.i,r*x.i+i*x.r);}
}a[N],b[N],w[N];
int A,B,n,L,R[N];
void FFT(C a[],int n){
for (int i=0;i<n;i++)
if (R[i]>i)
swap(a[R[i]],a[i]);
for (int t=n>>1,d=1;d<n;d<<=1,t>>=1)
for (int i=0;i<n;i+=(d<<1))
for (int j=0;j<d;j++){
C tmp=w[t*j]*a[i+j+d];
a[i+j+d]=a[i+j]-tmp;
a[i+j]=a[i+j]+tmp;
}
}
int main(){
scanf("%d",&A);A++;
scanf("%d",&B);B++;
for (int i=0;i<A;i++)
scanf("%lf",&a[i].r);
for (int i=0;i<B;i++)
scanf("%lf",&b[i].r);
for (n=1,L=0;n<=A+B;n<<=1,L++);
for (int i=0;i<n;i++){
R[i]=(R[i>>1]>>1)|((i&1)<<(L-1));
w[i]=C(cos(2.0*i*PI/n),sin(2.0*i*PI/n));
}
FFT(a,n),FFT(b,n);
for (int i=0;i<n;i++)
a[i]=a[i]*b[i],w[i].i=-w[i].i;
FFT(a,n);
A--,B--;
for (int i=0;i<=A+B;i++)
printf("%d ",int(a[i].r/n+0.5));
return 0;
}
$FFT$ 虽然能快速处理卷积,但是它也有很大的弊端。精度问题有时会导致一些错误。而且,有许多题目涉及了取模,比如 $998244353$ ,复数域下的 $DFT$ 精度更是暴露无遗。于是考虑是否有模意义下的这种算法。于是,便出现了快速数论变换($Fast Number-Theoretic Transform, FNT$)。
虽然之前列举了一些单位根的性质,但是 $FFT$ 用到的却和我列举的有些差别。
于是我们回顾一下 $FFT$ 利用了单位根的什么性质。
1. $omega_{n}^{n}=1$
2. $omega_{n}^{0},omega_{n}^1,cdots,omega_{n}^{n-1}$ 互不相同,满足了点值表示的条件。
3. $omega_n^2=omega_{frac{n}{2}}, omega_n^{frac{n}{2}+k}=-omega_n^k$ ,这个是分治的基础。
4. $omega_{n}^{-k}=conj(omega_n^k)$
$sum_{k=0}^{n-1}(omega_n^{j-i})^k=egin{cases}0& ext{$(i eq j)$}\n& ext{$(i=j)$}end{cases}$
这个是$IDFT$的基础。
原根
我们需要找满足上面的性质的整数。
于是我们找到了原根。
对于一个质数 $p$ ,其 原根 $g$ 满足 $g^0,g^1,g^2,cdots,g^{p-2}$ 在模 $p$ 意义下两两不同。
可以发现, $n$ 需要是 $p-1$ 的因数,才能满足条件。由于 $n$ 是 $2$ 的幂,所以对 $p$ 也有一定的要求。
$p$ 得是形如 $rcdot 2^k+1$ 的素数,其中 $2^kgeq n$ 。
有一些非常常见的 $NTT$ 模数:
$998244353=119 imes 2^{23}+1$ ,原根为 $3$ 。
$1004535809=479 imes 2^{21}+1$ ,原根为 $3$ 。
更多 $NTT$ 模数 $Longrightarrow$ http://blog.miskcoo.com/2014/07/fft-prime-table
现在我们来证明一下原根满足上面的那些性质。
令 $g_n^nequiv 1 pmod p$ 且 $g_n ^ 0,g_n ^ 1,cdots g_n ^ {n-1}$ 互不相同,则 $g_n equiv g^r pmod p$(这里的 $r=(p-1)/n$ 与之前提到的无关),等价于 $omega_n$ 。
1. $omega_{n}^{n}=1$
根据定义,显然成立。
2. $omega_{n}^{0},omega_{n}^1,cdots,omega_{n}^{n-1}$互不相同
根据原根的定义,也显然成立。
3. $omega_n^2=omega_{frac{n}{2}}, omega_n^{frac{n}{2}+k}=-omega_n^k$
由于 $g_nequiv g^r pmod p$ ,其中由于 $nr=p-1$ ,当 $n$ 取 $frac n2$ 时, $r$ 取 $2r$ ,所以 $g_{frac n2}equiv g^{2r}equiv(g^r)^2equiv g_n^2 pmod p$ 。
由费马小定理可得 $g^{p-1}-1equiv (g^{frac{p-1}2}+1)(g^{frac{p-1}2}-1)equiv 0pmod p$ ,所以 $g^{frac{p-1}2}equiv pm 1pmod p$ 。又由于 $g$ 为原根,满足第 $2$ 条性质。由于 $g^0equiv 1pmod p$ ,所以 $g^{frac{p-1}2}equiv -1pmod p$ 。于是:
$$g_{n}^{frac n2}equiv g^{frac{p-1}2}equiv -1pmod p$$
即 $g_n^{frac n2+k}equiv g_n^k imes g_n^{frac n2}equiv -g_n^kpmod p$ 。
4. $sum_{k=0}^{n-1}(omega_n^{j-i})^k=egin{cases}0& ext{$(i eq j)$}\n& ext{$(i=j)$}end{cases}$
由于 $4$ 的第一项不是很重要,所以可以不管(直接逆元算算就好了)。
$$sum_{k=0}^{n-1}g_n^{k(j-i)}equivegin{cases}n& ext{$(i=j)$}\ sum_{k=0}^{n-1}(g_{n}^{j-i})^kequivfrac{1-(g_{n}^{j-i})^n}{1-g_{n}^{j-i}}equiv 0 & ext{$(i eq j)$}end{cases}pmod p$$
于是,综上所述,原根满足了 $FFT$ 要用到的单位根的性质,于是我们可以把单位复根替换成原根,再写个和 $FFT$ 差不多的就可以了。
NTT参考代码 - 51Nod1028 大数乘法 V2
#include <cstdio>
#include <algorithm>
#include <cstdlib>
#include <cmath>
#include <cstring>
using namespace std;
typedef long long LL;
const LL mod=998244353;
const int N=1<<20;
LL Pow(LL x,LL y){
if (!y)
return 1LL;
LL xx=Pow(x,y/2);
xx=xx*xx%mod;
if (y&1LL)
xx=xx*x%mod;
return xx;
}
LL A,B,a[N],b[N],R[N],g[N],n,L;
char str[N];
void read(){
scanf("%s",str);
A=strlen(str);
for (int i=0;i<A;i++)
a[A-i-1]=str[i]-'0';
scanf("%s",str);
B=strlen(str);
for (int i=0;i<B;i++)
b[B-i-1]=str[i]-'0';
}
void NTT(LL a[N],int n){
for (int i=0;i<n;i++)
if (i<R[i])
swap(a[i],a[R[i]]);
for (int d=1,t=n>>1;d<n;d<<=1,t>>=1)
for (int i=0;i<n;i+=(d<<1))
for (int j=0;j<d;j++){
LL tmp=g[t*j]*a[i+j+d]%mod;
a[i+j+d]=(a[i+j]-tmp+mod)%mod;
a[i+j]=(a[i+j]+tmp)%mod;
}
}
int main(){
read();
for (n=1,L=0;n<=A+B;n<<=1,L++);
for (int i=0;i<n;i++)
R[i]=(R[i>>1]>>1)|((i&1)<<(L-1));
g[0]=1,g[1]=Pow(3,(mod-1)/n);
for (int i=2;i<n;i++)
g[i]=g[i-1]*g[1]%mod;
NTT(a,n),NTT(b,n);
for (int i=0;i<n;i++)
a[i]=a[i]*b[i]%mod;
g[0]=1,g[1]=Pow(g[1],mod-2);
for (int i=2;i<n;i++)
g[i]=g[i-1]*g[1]%mod;
NTT(a,n);
LL Inv=Pow(n,mod-2);
for (int i=0;i<n;i++)
a[i]=a[i]*Inv%mod;
for (int i=0;i<n-1;i++)
a[i+1]+=a[i]/10,a[i]%=10;
int d;
for (d=n-1;d&&!a[d];d--);
for (int i=d;i>=0;i--)
putchar(a[i]+'0');
return 0;
}
顾名思义,分治 $FFT$ 就是分治再加上 $FFT$ 嘛。
考虑有如下的递推式:
$$a_i=sum_{j=1}^{i}k_ja_{i-j}$$
其中 $k$ 数组以及 $a_0$ 给出。
我们发现这个式子非常像多项式卷积的形式,但是显然不能所有的 $a_i$ 一起计算,就是说一次 $FFT$ 显然不能解决问题。
于是我们可以分治 $FFT$ 。
定义 $solve(L,R)$ 为“在 $L$ 之前的 $a_i$ 都已经得到答案的基础上完成 $L$ ~ $R$ 的计算”。
于是,我们可以写出下面的这个伪代码:
过程 solve(L,R) |----mid←(L+R)/2 |----solve(L,mid) |----FFT(a[L...mid]×k[1...R-L]→a[mid+1...R]) |----solve(mid+1,R) 过程结束
其中在写代码的时候边界情况可能会有所不同。
但是读者请注意,上面 $FFT()$ 里处理的不是右区间受到的全部贡献,只是完成了左区间对于右区间的贡献,事实上,一个 $a_i$ 会分成大约 $O(log n)$ 次来贡献。
拆系数$FFT$和三模数$NTT$毛啸2016的集训队论文有写,本节内容许多摘自他的论文,读者可以直接查阅他的论文。
经典的 $FFT$ 的虽然很好用,但是在一些数据范围较大的题目之下,还是要挂。
当两个长度为 $10^5$ 级别的序列卷积,模数为 $10^9$ 级别(不为 $NTT$ 模数),直接 $FFT$ 的话,每个数的结果大约在 $10^{23}$ 左右,超出了 $2^{64}$ ,一方面会使浮点数出现较大的误差,一方面你也不可能把他转成 $64$ 位整形然后取模,这个时候就要用下面的两种方法了。
拆系数$FFT$
我们设 $M$ 为模数的大小,则取 $M_0=leftlceilsqrt{M} ight ceil$ ,根据带余除法将所有的 $x$ 表示成 $x=k[x]M_0+b[x]$ 。其中 $k[x]$ 和 $b[x]$ 为整数。
我们假设多项式 $A(x)$ 的系数序列为 $a_i$ ,多项式 $B(x)$ 的系数序列为 $b_i$ ,那么我们把 $k[a_i],b[a_i],k[b_i],b[b_i]$ 形成的四个序列两两卷积,卷积结果大约在 $10^{14}$ 级别,可以接受。并先取个模,然后乘上相应的系数,一起加到答案里面就可以了。这样要 $7$ 次 $(I)DFT$ 。通过 myy 论文里面讲的优化方法可以优化到 $4$ 次甚至 $3.5$ 次$DFT$。
三模数$NTT$
我们找 $3$ 个大小在 $10^9$ 级别的 $NTT$ 模数。然后分别在这三个模数意义下求卷积结果,然后中国剩余定理合并即可。
具体方法:我们假设模数分别是 $mod_0,mod_1,mod_2$ ,先合并前两个模数,也就是求出答案在模 $mod_0 imes mod_1$ 意义下的值,然后用逆元将模 $mod_0 imes mod_1 imes mod_2$ 意义下的数,也就是答案表示成 $k imes mod_0 imes mod_1+b$ 的形式,这个东西我们不必真正求出,我们只需要在模 $M$ 意义下求即可,这样只需要使用 $64$ 位整型即可。
但这个需要 $9$ 次 $DFT$ 效率没有上面的那个快。
(而且博主太菜了没写过,目前只写过 $9$ 次 $DFT$ 的拆系数 $FFT$ (截至2018-04-17))
套路与例题以下例题的链接是详细题解,题解里面有题目链接
套路1 - 字符串匹配
当我们从母串的某一个位置开始和模式串匹配的时候:
首先,我们发现需要匹配的字符对的下标差会是定值,所以我们一般会把其中一个字符串进行翻转,因为翻转之后,需要匹配的字符对的下标之和为定值,这样才能满足卷积形式。(下面是翻转字符串之后,匹配连线的示意图)

放例题:
(注意,在此之后,我默认你已经能对是否翻转有敏感的认识)
BZOJ4053 两个串
题意
给定两个字符串 S 和 T ,回答 T 在 S 中出现了几次,在哪些位置出现。注意 T 中可能有 ? 字符,可以匹配任何字符。串长 $leq 10^5$
提示
考虑到有通配符 $?$ ,我们不能直接 KMP 。
但是我们可以通过构造卷积,通过判断卷积结果的某一位是否为 0 来确定某一个位置开始是否可以匹配。
可以从相同字符值差为 0 以及通配符与其他字符永远匹配方面来考虑。
第一道题,可以看看题解。
BZOJ4259 残缺的字符串
题意
给你两个串,用其中一个来匹配另一个。问从母串的那些位置开始可以匹配模式串。注意有"*"可以匹配任何字符。
串长 $leq 3 imes 10^5$ 。
提示
和上一题唯一的区别就是两个串中都有通配符。基本上一样的。只是要稍微卡下时间和空间。
CodeForces 528D Fuzzy Search
题意
给你两个串 $A,B(|A|geq|B|)$ ,以及一个 $k$ 。
其中 $A_i$ 与 $B_j$ 匹配的条件是 $A_{i-kdots i+k}$ 中至少有一个与 $B_j$ 相同。
问 $B$ 能在 $A$ 中匹配多少次。
字符集: ${'A','C','G','T'}$ 。
$|B|leq|A|leq 2 imes 10^5,kleq 2 imes 10^5$
提示
可以预处理每一个位置可以匹配到 ${'A','C','G','T'}$ 的哪些。
然后,如果按照之前两题的套路来构造卷积,先不谈常数巨大,手工展开都很困难。
注意到字符集非常小,我们可以考虑对于每一个字符分开考虑,构造卷积。
套路2 - 卷积形式变形
BZOJ3527 [ZJOI2014]力
题意
给出长度为 $m$ 的序列 $q_{1..m}$ ,让你输出长度为 $m$ 的序列 $E_{1..m}$ 。
其中:
$$E_i=sum_{j=1}^{i-1}frac{q_j}{(i-j)^2}-sum_{j=i+1}^{m}frac{q_j}{(i-j)^2}$$
提示
将原式写成两个卷积式。其中一个很容易 $FFT$ ,另外一个可以通过翻转和更改求和指标等一系列推导变成 $FFT$ 擅长的卷积形式。
套路3 - 背包问题相关
有时候,我们会碰到类似无限背包的问题。给定一些物品的体积,问用这些物品可以拼出某个范围内的哪些体积。
构造多项式:如果有体积为 $i$ 的物品,则 $i$ 次项系数为 $1$ ,否则为 $0$ 。特别的,我们手工添加一个 $0$ 体积的物品。然后多项式平方一下,有值的位置所代表的体积就是可以通过至多 $2$ 个体积值相加得到。然后我们顺手把所有有值的改成 $1$ 。再平方,得到的是至多 $4$ 个体积值相加得到的体积。平方 $k$ 次,就能得到至多 $2^k$ 个物品体积相加可以得到的所有体积。复杂度 $O(nlog^2 n)$ 。其中 $n$ 为体积范围。
CodeForces 268E Ladies' Shop
题意
首先,给你 $n$ 个数(并告诉你 $m$ ),分别为 $p_{1dots n}$ 。
让你求一个数的集合,满足:
当且仅当从这个数的集合中取数(可以重复)求和时(设得到的和为 $sum$ ),如果 $sumleq m$ ,则数 $sum$ 在给你的 $n$ 个数之中。
如果没有这种集合,输出 $NO$ 。
否则,先输出 $YES$ ,然后输出这个集合最小时的元素个数,并输出集合中的所有元素。
$1leq n,mleq 10^6,1leq p_ileq 10^6$
提示
考虑思考本题的特殊性,在本题之前的小例子的基础上,舍去无用的运算。
套路4 - 分治$FFT$
BZOJ4836 [Lydsy1704月赛]二元运算
题意
定义二元运算 $opt$ 满足
$$x opt y=egin{cases}x+y & ext{$(x<y)$} \ x-y & ext{$(xgeq y)$}end{cases}$$
现在给定一个长为 $n$ 的数列 $a$ 和一个长为 $m$ 的数列 $b$ ,接下来有 $q$ 次询问。每次询问给定一个数字 $c$ 你需要求出有多少对 $(i, j)$ 使得 $a_i opt b_j=c$ 。
提示
在分治 $a_i$ 的值域的时候,左右区间内的数会满足左区间严格小于右区间,这是个很好的性质,会便于你按照上面的式子分类贡献, $FFT$ 优化。
CodeForces 553E Kyoya and Train
题意
一个有 $n$ 个节点 $m$ 条边的有向图,每条边连接了 $a_i$ 和 $b_i$ ,花费为 $c_i$ 。
每次经过某一条边就要花费该边的 $c_i$ 。
第 $i$ 条边耗时为 $j$ 的概率为 $p_{i,j}$ 。
现在你从 $1$ 开始走到 $n$ ,如果你在 $t$ 单位时间内(包括 $t$ )到了 $n$ ,不需要任何额外花费,否则你要额外花费 $x$ 。
问你在最优策略下的期望花费最小为多少。
(注意你每走一步都会根据当前情况制定最好的下一步)
提示
本题是 myy 的论文题,思维含量较大。
首先我告诉你 $O(mTlog^2 T)$ 的复杂度可以过。
先考虑 $DP$ ,然后通过设一个期望贡献累加器,来化简 $DP$ 转移方程,并从中挖掘 $FFT$ 擅长的卷积形式,并通过分治 $FFT$ 优化。
杂题
BZOJ3160 万径人踪灭
题意
给你一个只含 $a,b$ 的字符串,让你选择一个子序列,使得:
$1.$ 位置和字符都关于某一条对称轴对称。
$2.$ 不能是连续的一段。
问原来的字符串中能找出多少个这样的子序列。答案对 $10^9+7$ 取模。
串长 $leq 10^5$ 。
提示
先避开条件2考虑如何解题。考虑一个点为中心,在其两侧能互相匹配的字符对数。每一对可以互相匹配的都可以选择选或者不选。从中寻找卷积形式。
对于不满足2的,显然是连续回文子串个数, $Manachar$ 裸题。
BZOJ4451 [Cerc2015]Frightful Formula
题意
给你一个 $n imes n$ 矩阵的第一行和第一列,其余的数通过如下公式推出:
$$f_{i,j}=acdot f_{i,j-1}+bcdot f_{i-1,j}+c$$
求 $f_{n,n}mod (10^6+3)$ 。提示
考虑每一个格子各自对于 $f_{n,n}$ 的贡献。
对于除了第一行和第一列的格子,性质相似,可以列出求和式子。再通过推导,寻找利于 $FFT$ 的卷积形式。
BZOJ4827 [Hnoi2017]礼物
题意
有两个长为 $n$ 的序列 $x$ 和 $y$ ,序列 $x,y$ 的第 $i$ 项分别是 $x_i,y_i$ 。
选择一个序列 $A$ ,现在你可以对它进行如下两种操作:
$1.$ 得到一个和 $A$ 循环同构的序列 $A'$ 。
$2.$ 给所有的 $A'_i$ 都加上 $c(cin N^+)$ ,得到序列 $A''$ 。
你进行上面两个操作之后,得到的序列分别为 $x'',y''$ (注意 $x,y$ 两个序列中至少有一个序列没有发生任何变化)
序列 $x''$ 和 $y''$ 的差异值为
$$sum_{i=1}^{n}(x''_i-y''_i)^2$$
问差异值最小为多少。
提示
考虑先写出一个一般的结果式子,然后略微展开,得到一些常数,一个关于 $c$ 的二次函数和一个卷积式。
对于二次函数我们求一下最值即可。
对于卷积式,我们考虑求其最值。先倍长某一个串,再翻转某一个串, $FFT$ 优化,计算出你需要的东西。
CodeForces 958F3 Lightsabers (hard)
题意
有 $n$ 个球,球有 $m$ 种颜色,分别编号为 $1cdots m$ ,现在让你从中拿 $k$ 个球,问拿到的球的颜色所构成的可重集合有多少种不同的可能。
注意同种颜色球是等价的,但是两个颜色为 $x$ 的球不等价于一个。
$1leq nleq 2 imes 10^5, 1leq m,kleq n$。
提示
一道比较新的题目,是我写这篇博文前几天的 $CodeForces$ 上的 $ACM$ 比赛题。
考虑构造一些小的多项式,然后把他们全部乘起来得到最终的解。
需要分治或者启发式合并优化。建议启发式合并。
CodeForces 623E Transforming Sequence
题意
给定 $n,k$ 。
让你构造序列 $a(0<a_i<2^k)$ ,满足 $b_i(b_i=a_1 or a_2 or cdots or a_i)$ 严格单调递增。( $or$ 为按位或)
问你方案总数。对 $10^9+7$ 取模。
$nleq 10^{18},kleq 30000$
提示
又是一道 myy 论文题。
思维含量也挺大的。
先考虑暴力 $DP$ ,然后考虑加大转移的步长,从已经得到的 $dp$ 值中状态转移得到新的 $dp$ 值。需要寻找你得到的加大步长后的 $dp$ 转移方程的利于 $FFT$ 的卷积形式,然后倍增 $FFT$ 优化。
参考文章与博客&鸣谢
(特别鸣谢)http://blog.miskcoo.com/2015/04/polynomial-multiplication-and-fast-fourier-transform#comment-37058
2016国家队候选队员论文 - 毛啸 - 再探快速傅里叶变换
《多项式导论》 - picks
https://oi.men.ci/fft-notes/
http://picks.logdown.com/posts/177631-fast-fourier-transform
http://picks.logdown.com/posts/247168-fast-fourier-transform-modulo-prime
后记写了好几天真累啊。感谢所有给我提供帮助的文章、博客,以及写它们的人,以及读完这篇学习笔记、看到这里的你。
希望这篇博文能带给您帮助。
由于博主学识短浅,如果您在阅读的过程中发现任何错误,麻烦您在百忙之中给我留言指出,谢谢。
当然,多项式的运用远不止于此。关于多项式求逆、多项式除法、多项式开根、多项式 exp/ln 、多项式求导/求不定积分、牛顿迭代、泰勒展开等等,也许我会陆续推出关于这些算法学习笔记,敬请期待。
UPD(2018-04-18 15:00):自行验稿一遍,修改了约 10 处细节错误,比如空格没打或者同于打了等于这类的,以及一处 $DFT$ 写成了 $FFT$ ,均已修改。
UPD(2018-04-19 15:15):发现有一个题意概括里的细节错误,已经改正。
UPD(2018-04-20 20:06):感谢 Emoairx 指出,博主当时手残了,把拉格朗日插值法的复杂度写错了。现在已经修改。
UPD(2018-07-15 20:24):修正 3 处错误。
UPD(2018-09-23 18:45):补上了一个漏打的字